1. Párhuzamosítás, algoritmusok
A párhuzamosítás szükségessége
Moore törvénye
Gordon Earle Moore, Intel társalapítója, 1965.
A chip-ekben a tranzisztorok száma 18-24 havonat duplázódik.
A törvény 1971-2011 mindenképpen érvényben volt.
https://en.wikipedia.org/wiki/Moore%27s_law
Fizikális korlátok
Az elemi, elektromos számítási egységek sebessége tovább már nem növelhető.
Magasabb órajelhez nagyobb feszültség kell. \(\rightarrow\) Tápellátási és hűtési problémák.
A vezetékek lehetséges vastagsága elérte a minimális limitet.
A számítási teljesítmény növelésére alapvetően a számítási egységek növelésével van lehetőség.
Free lunch
Régebben lehetett arra hagyatkozni, hogy az új gépeken a szoftverek gyorsabban fognak tudni futni.
Aktuálisan ez csak párhuzamosítással oldható meg.
További szempontok
A számítási teljesítmény mellett a memória és tár is szükségessé teheti elosztott rendszer kialakítását.
Bizonyos számításoknál a redundancia is szempont lehet. (Például blokkláncok, felhasználókhoz kiszervezett számítások.)
Adott feladat gyorsabb megoldásán túl szempont lehet a korábbiaknál lényegesen nagyobb problémák megoldását kitűzni célul.
A probléma nagysága jelenthet nagyobb számítási pontosságot is (például szimulációk, előrejelzések esetében).
Egyre nagyobb mennyiségű adat áll rendelkezésre (például képek, videók, szenzoradatok).
Programok párhuzamosítása
Lényegesen más megközelítést igényel. Más eszközök kellenek. Más problémák jelentkeznek.
Gyakran az algoritmus egészét érinti a változás.
Egyfajta érdekes optimalizálási problémáról beszélhetünk.
Alapfogalmak
Konkurrens
A feladatok végrehajtása időben átfedésben van.
Például a második feladat hamarabb kezdődik, mint hogy az első véget ért volna.
Párhuzamos
A végrehajtás időben egyszerre történik.
Szimultán, szinkron
Figyelem
A konkurrens végrehajtás jelenthet aszinkron vagy időosztásos működést is!
\(\rhd\) Adjunk példát olyan konkurrens végrehajtásra, amely nem párhuzamos!
Flynn-féle osztályozás
Michael J. Flynn, 1966.
SISD, SIMD, MISD, MIMD
Memóriamodellek
\(\rhd\) Gondoljuk át a memória és a számítási elemek közötti 1:N, N:1, N:M kapcsolatokat!
Lokális memória
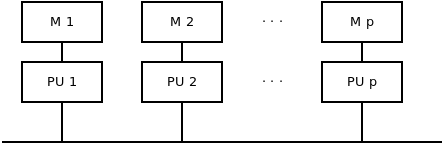
Cache
Cache update probléma
Moduláris memória
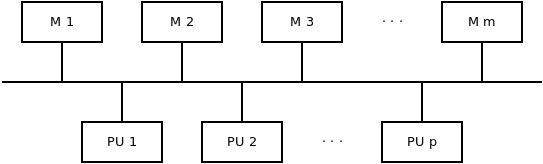
Osztott memória
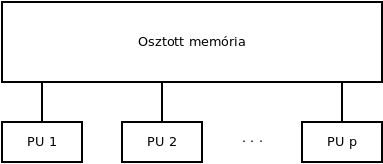
Kritikus szakasz
Kölcsönös kizárás
Párhuzamos gép modellek
PRAM modell
PRAM: Parallel Random Access Machine
PU: Processing Unit
Egy absztrakt modellről van szó.
A PU-k száma tetszőleges sok lehet.
A memória méretére vonatkozóan nem ad meg limitet.
Minden PU szimultán hozzá tud férni a memóriához.
(Ezek a feltételezések valós gépek esetén sajnos nem állnak fenn.)
A modellt a memóriához való hozzáférés alapján tovább szokták pontosítani.
CREW: Concurrent Read - Exclusive Write
Egy adott memóriacellát minden PU tud olvasni tetszőleges időpontban, viszont
egyszerre csak egy tudja írni.
CRCW: Concurrent Read - Concurrent Write
Feltételezi, hogy mindegyik PU egyszerre tud olvasni és írni is egy adott memória cellát. Ez az érték beállítása szempontjából problémás lehet, ezért erre vonatkozóan külön megközelítések vannak.
tetszőleges mód: Nincs definiálva, hogy konkurrens hozzáférés esetén mi fog történni. Egy nem-determinisztikus gépet kapunk így.
konzisztens mód: Mindegyik PU-nak ugyanazt az értéket lehet csak beírnia.
prioritásos mód: A PU-k között van egy sorrend, amely alapján mindig eldönthető, hogy ütközés esetén melyiknek az értéke kerül be a memóriába.
fúziós mód: Egyidejű írás esetén egy aggregálást hajt végre. A művelet kommutatív és asszociatív kell, hogy legyen, mint például a minimum, maximum, AND, OR, szummázás műveletek.
EREW: Exclusive Read - Exclusive Write
Ez a leginkább realisztikus modell.
Egyidejűleg egy cellához csak egy PU férhet hozzá.
\(\rhd\) Melyik kombináció maradt ki? Mi lehet annak az oka?
Számítási költség és hatékonyság
Vezessük be a következő jelöléseket!
\(P\): a megoldandó probléma
\(n\): a probléma mérete
\(T_{\text{seq}}(n)\): számítási idő szekvenciális végrehajtás esetén
\(T_{\text{par}}(p, n)\): számítási idő párhuzamos végrehajtás esetén \(p\) darab PU-val.
Költség (Cost)
Munka (Work)
\(W_p(n)\): Az összes PU-n elvégzett műveletek összege.
Ideális esetben a munka és a költség meg kellene, hogy egyezzen.
A költség akkor lesz minimális, hogy ha minden PU hasznosan tölti az időt (nem várakozik).
Szekvenciális esetben a kettő megegyezik. (Ez tekinthető a \(p = 1\) esetnek is.)
Gyorsítás (Speed-Up)
Ideális esetben a párhuzamos végrehajtás gyorsabb, mint a szekvenciális, így egy 1-nél nagyobb értéket kapunk.
A mennyiséget gyakran százalékos formában használják.
Hatékonyság (Efficiency)
\(\rhd\) A definiált értékekből hogyan lehetne egyszerűen kiszámítani a hatékonyságot?
\(\rhd\) Milyen intervallumon változhat a hatékonyság értéke?
A hatékonyság romlásának lehetséges okai:
Kiegyenlítetlenség
Kommunikációs költség, adminisztrációs költség (overhead)
\(\rhd\) Miért lehet fontos a futási idő és a gyorsítás mellett a hatékonysággal is foglalkozni?
Komplexitás mérése
\(\rhd\) Milyen ordo szimbólumok vannak, és mit jelentenek?
Párhuzamos komplexitás:
\(\rhd\) A kifejezésben hogy jelenik meg a problémaméret?
Szimuláció kevesebb PU-val
Tegyük fel, hogy egy \(\mathcal{A}\) algoritmust egy \(p\) darab PU-val rendelkező PRAM gépen \(t\) idő alatt oldunk meg. Ugyanezen számítás egy azonos típusú gépen \(p' \leq p\) számú PU-val szimulálható \(\mathcal{O}\left(t \cdot \dfrac{p}{p'}\right)\) idő alatt.
A \(p'\) számú PU-val rendelkező gép költsége legfeljebb duplája lesz a \(p\) számú PU-val rendelkezőjének.
Bizonyítás
Az \(\mathcal{A}\) algoritmus minden lépése \(\left\lceil\dfrac{p}{p'}\right\rceil\) időegység alatt szimulálható a \(p'\) PU-val a konkurrens részek szekvenciálissá tételével.
Mivel az eredeti számítás \(t\) időegységig tartott, ezért a szimulált \(t \cdot \left\lceil\dfrac{p}{p'}\right\rceil\) lesz, amelyből megkapjuk, hogy az időbonyolultság \(\mathcal{O}\left(t \cdot \dfrac{p}{p'}\right)\).
Számítsuk ki a \(p'\) PU-val rendelkező gép költségét! Jelölje \(t'\) ennek a gépnek a számítási idejét!
Így tehát azt kapjuk, hogy
Brent tétele
Tegyük fel, hogy egy \(\mathcal{A}\) algoritmus összesen \(m\) művelet végrehajtásával jár, és \(t\) ideig tart. Ugyanezen típusú gépen, \(p\) darab PU-val \(\mathcal{O}\left(\dfrac{m}{p} + t\right)\) idő alatt szimulálható.
Bizonyítás
Tegyük fel, hogy az \(\mathcal{A}\) algoritmus az \(i\)-edik lépésben \(m(i)\) műveletet hajt végre. Az összes lépést elvégezve ez visszaadja \(m\)-et:
Az \(i\)-edik lépés szimulálható \(\left\lceil\dfrac{m(i)}{p}\right\rceil\) időegység alatt, amelyre fennáll, hogy
Könnyen látható, hogy
amelyből adódik a tétel állítása. \(\square\)
Amdahl törvénye
Gene Amdahl, 1967.
Azt mutatja meg, hogy egy program esetében a párhuzamosítható részek arányát ismerve ideális esetben mennyi lesz a gyorsítás (speedup) értéke.
A probléma méretét rögzítettnek tekinti.
Egy felső becslésről van szó.
Használjuk a következő jelöléseket!
\(p\): a számítási egységek száma
\(f\): a program egészére nézve a párhuzamosítható részek aránya
Figyelem
A törvény elméleti felső korlátot ad!
\(\rhd\) Vizsgáljuk meg az \(f \rightarrow 0\) és az \(f \rightarrow 1\) eseteket!
\(\rhd\) Mennyinek kell lennie legalább a párhuzamosítható részek arányának, hogy ha legalább 10-szeres gyorsítást szeretnénk elérni?
\(\rhd\) Mennyi lesz ez 1000-szeres gyorsítás esetében?
\(\rhd\) Tegyük fel, hogy egy algoritmusban a párhuzamosítható részek aránya 80%. Legalább mennyi számítási egységre van szükségünk, hogy 4-szeres gyorsítást el tudjunk érni?
\(\rhd\) Ábrázoljuk az összefüggést!
Gustafson-Barsis törvény
John L. Gustafson, Edwin H. Barsis, 1988.
Tetszőlegesen nagy méretű problémát feltételez.
Használjuk a következő jelöléseket!
\(p\): a számítási egységek száma
\(f\): a program egészére nézve a párhuzamosítható részek aránya
\(\rhd\) Tegyük fel, hogy van egy 64 számítási egységet tartalmazó számítógépünk! Feltételezve, hogy tetszőlegesen sok időnk lehet, maximálisan mennyi lehet a gyorsítás mértéke, hogy ha a program 90%-a párhuzamosítható?
\(\rhd\) Tegyük fel, hogy egy program 60%-a párhuzamosítható! A Gustafson-Barsis törvény alapján legalább mennyi számítási egységre van szükségünk, hogy 40-szeres gyorsítást tudjunk elérni?
\(\rhd\) Ábrázoljuk az összefüggést!
Párhuzamosság ábrázolása
\(\rhd\) Adjunk példákat, hogy hol szoktak ilyen ábrázolási módokat használni!
Gantt diagram
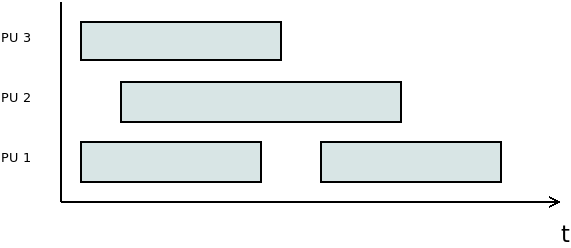
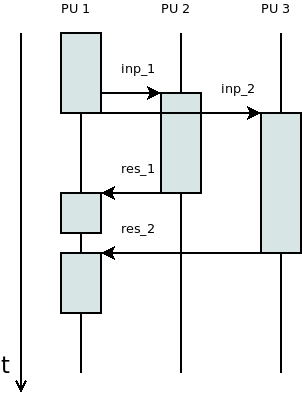
Szekvencia diagram
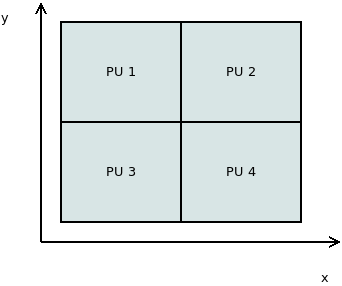
Problématér felosztása
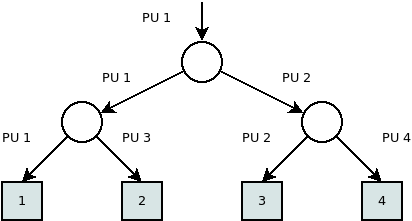
Hívási fa
Elsősorban nem párhuzamos végrehajtást szokás vele ábrázolni.
Az „Osszd meg és uralkodj!” elv szerint a problématér felosztása (főleg rekurzív esetekben) nagyon szépen ábrázolható vele.
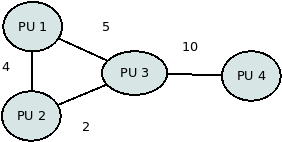
Hálózati topológia, sávszélesség
Elterjedt topológiák
Busz
Gyűrű
Rács
Tórusz
Hiperkocka
Fa
Fat-tree
Elvileg tetszőleges gráf lehetne a topológia. Ezek elvi és praktikus okok miatt alakultak így.
Elvek és modellek
Osszd meg és uralkodj elv
Felosztás \(\rightarrow\) művelet \(\rightarrow\) egyesítés
Tipikusan rekurzív formában használatos
Figyelem
A felosztás megfelelő szintjének meghatározása külön érdekes problémakör! (Jellemzően nem szerencsés az elemek szintjéig lemenni.)
Pipeline párhuzamosítás
Tegyük fel, hogy vannak feldolgozandó elemeink, amelyeken adott sorrendben, mindig ugyanazokat a lépéseket kell végrehajtani.
Feltételezzük, hogy a lépések végrehajtási ideje közel egyenlő.
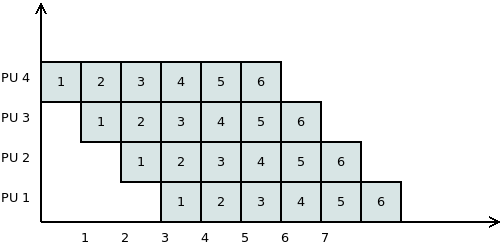
Mekkora gyorsítást tudunk így elérni?
Mennyire lesz ez a módszer hatékony?
Termelő-fogyasztó probléma
Task pool
Gyors válaszidő, terhelés kiegyenlítés érdekében használják például.
Általában sort használnak hozzá.
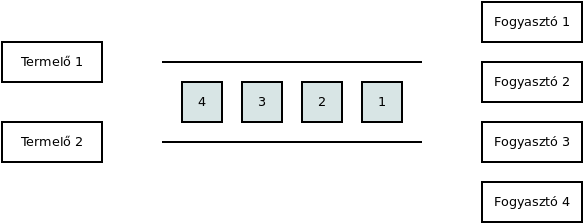
Milyen előnyei vannak a módszernek?
Milyen eseteket nem tud jól kezelni?
Számítási példák
Alapvető értékek meghatározása
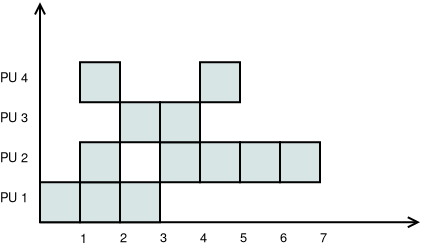
Számítsuk ki a költség, munka, gyorsítás és hatékonyság értékeket!
Feladatmegosztás optimalizálása
Tegyük fel, hogy adott 2 gép, melyek hálózaton keresztül tudnak kommunikálni.
A feladatokat egységnyieknek tekintjük.
Összesen 3000 feladat van.
Az első gép 1 feladatot 10 másodperc alatt old meg, a második pedig 5 másodperc alatt.
A bemenet az első gépen áll rendelkezésre.
A második gépre való küldés 2 másodpercet igényel feladatonként.
A küldés és fogadás ideje alatt a gépek nem tudnak lényegi számítást végezni.
Az eredményeknek az első gépre kell kerülniük.
Hogyan ossza meg a két gép a feladatokat, hogy a lehető legkevesebb ideig tartson összességében?
Vezessünk be jelöléseket!
Próbáljuk meg általánosan is megoldani a problémát!
Ábrázoljuk grafikonon a párhuzamos végrehajtás idejét!
Algoritmusok
Leképzés (map)
Az egyik legegyszerűbb és leghatékonyabban párhuzamosítható algoritmus.
Tegyük fel, hogy adott egy \(x \in \mathbb{R}^n\) vektor! Ki szeretnénk számítani egy \(y \in \mathbb{R}^n\) vektort, melyre teljesül, hogy \(y_i = f(x_i), \forall i\), és \(f: \mathbb{R} \rightarrow \mathbb{R}\) egy tetszőleges valós függvény.
Hogyan változik a munka, költség, gyorsítás és hatékonyság \(p\) függvényében?
Aggregálás
Legyen adott egy \(n\) elemű sorozat.
Aggregálni szeretnénk az értékeket egy bináris, kommutatív, asszociatív művelettel (például: összeadás, szorzás, minimum- és maximum számítása).
A szekvenciális algoritmus ezt csak \(\mathcal{O}(n)\) idő alatt képes kiszámítani.
Mutassuk meg, hogy ez párhuzamosítással gyorsabban is megoldható!
Vizsgáljuk meg, hogy \(n = 16\) elem esetében hogyan történhet a végrehajtás!
Tekintsük át a \(p = 1, 2, \ldots, 16\) eseteket!
Számítsuk ki a munka, költség, gyorsítás és hatékonyság értékeket!
Elem keresése egy sorozatban
A sorozatról nem feltételezünk rendezettséget.
Egy elem létezését vagy annak indexét szeretnénk meghatározni.
A probléma nagyon hasonlóan kezelhető az aggregáláshoz.
Hogy ha csak egy elem létezését vizsgáljuk, és tetszőlegesen sok számítási egységünk van, akkor mi jelenti a szűk keresztmetszetet?
Adott tulajdonságú elemek száma
Szintén egy aggregálás jellegű műveletről van szó.
Összeget számolhatunk úgy, hogy az elemek szintjén először egy összehasonlítást végzünk.
Pi közelítése
Monte Carlo módszerrel
Rögzített felosztás alapú numerikus integrálással
Mátrix szorzás
Vektor-vektor szorzás
Vektor-mátrix szorzás
Mátrix-mátrix szorzás
Vizsgáljunk meg egy olyan esetet, ahol \(n = 3, m = 2, p = 4\). Feltételezzük, hogy egy CREW PRAM gépünk van.
Mennyi számításra lenne szükségünk szekvenciális esetben?
Milyen lehetőségek vannak párhuzamosításra?
Hogyan változik a számítási bonyolultság az egyes esetekben?
Összefésülő rendezés
Elevenítsük fel az összefésülés algoritmusát!
Vizsgáljuk meg az összefésülés, mint rekurzív algoritmus párhuzamosítását!
Nézzük meg, hogy a Batcher-féle páros-páratlan összefésülés milyen előnyökkel járna!
Vizsgáljuk meg a következő tömb rendezését!
Gyorsrendezés
A gyorsrendezés algoritmusa a problémateret rekurzívan 2 részre bontja.
Az egyes ágak külön is kiértékelhetőek.
Tűz szimuláció
Tegyük fel, hogy tűznek a lángjait szeretnénk szimulálni. A teret diszkretizáljuk úgy, hogy az aktuális hőmérsékletet egy \(T \in \mathbb{R}^{n \times m}\) méretű mátrixba tároljuk. Feltételezzük, hogy a hő felfelé (a nagyobb indexű soroktól az alacsonyabbak felé) terjed.
A peremfeltételek a mátrix alsó és oldalsó részein adottak. A bal- és jobb oldali szélen konstans 0-nak tekintjük.
A hőmérséklet értékeket a \((k+1)\)-edik iterációban a következő összefüggés szerint számolhatjuk:
Quatropoly
Mezők egyidejű kiértékelése
Fában való keresés
Amőba
Állapot kiértékelés
Fa bejárás
Paraméterek optimalizálása
Floodfill algoritmus
Tekinthető egy összefüggő részgráf keresési problémájának is.
A számítási része egyszerű.
Az adatok szinkronizálása, gyűjtése jelent kihívást.
Konvex burok számítása
Quickhull
Mergehull
Genetikus algoritmus párhuzamosítása
Minden egyed jósági (fittness) értékét párhuzamosan ki lehet számítani.
A jósági érték alapján a rendezés párhuzamosítható.
Kereszteződést követően az új egyedek időben egyszerre létrehozhatók.