1. Előadás - Alapfogalmak, tételek

A párhuzamosítás szükségessége

Moore törvénye

• Gordon Earle Moore, Intel társalapítója, 1965.

• A chip-ekben a tranzisztorok száma 18-24 havonta duplázódik.

• A törvény 1971-2011 mindenképpen érvényben volt.

https://en.wikipedia.org/wiki/Moore%27s_law

Fizikális korlátok

• Az elemi, elektromos számítási egységek sebessége tovább már nem növelhető.

• Magasabb órajelhez nagyobb feszültség kell. \(\rightarrow\) Tápellátási és hűtési problémák.

• A vezetékek lehetséges vastagsága elérte a minimális limitet.

A számítási teljesítmény növelésére alapvetően a számítási egységek növelésével van lehetőség.

Free lunch

• Régebben lehetett arra hagyatkozni, hogy az új gépeken a szoftverek gyorsabban fognak tudni futni.

• Aktuálisan ez csak párhuzamosítással oldható meg.

További szempontok

• A számítási teljesítmény mellett a memória és tár is szükségessé teheti elosztott rendszer kialakítását.

• Bizonyos számításoknál a redundancia is szempont lehet. (Például blokkláncok, felhasználókhoz kiszervezett számítások.)

• Adott feladat gyorsabb megoldásán túl szempont lehet a korábbiaknál lényegesen nagyobb problémák megoldását kitűzni célul.

• A probléma nagysága jelenthet nagyobb számítási pontosságot is (például szimulációk, előrejelzések, renderelés esetében).

• Egyre nagyobb mennyiségű adat áll rendelkezésre (például képek, videók, szenzoradatok).

Programok párhuzamosítása

• Lényegesen más megközelítést igényel. Más eszközök kellenek. Más problémák jelentkeznek.

• Gyakran az algoritmus egészét érinti a változás.

• Egyfajta érdekes optimalizálási problémáról beszélhetünk.

Programozás szempontjából

• A programokkal szeretnénk kihasználni a rendelkezésre álló erőforrásokat.

• Az aktuálisan elérhető hardverek, rendszerek támogatják a párhuzamos végrehajtást.

• Az elosztott rendszerekben ugyanazok a párhuzamosításból, aszinkron végrehajtásból eredő problémák jelennek meg, mint amilyenekkel például több szálas programoknál egy programon belül, vagy egy gépen belül több folyamat esetében találkozhatunk.

Alapfogalmak

Konkurrens

• A feladatok végrehajtása időben átfedésben van.

• Például a második feladat hamarabb kezdődik, mint hogy az első véget ért volna.

Párhuzamos

• A végrehajtás időben egyszerre történik.

• Szimultán, szinkron

Figyelem

A konkurrens végrehajtás jelenthet aszinkron vagy időosztásos működést is!

\(\rhd\) Adjunk példát olyan konkurrens végrehajtásra, amely nem párhuzamos!

Flynn-féle osztályozás

• Michael J. Flynn, 1966.

• Single/Multiple, Instruction/Data

Lehetséges kombinációk

• SISD: Soros végrehajtás

• SIMD: Vektor processzorok

• MISD: Csővezeték elvű gépek

• MIMD: A párhuzamos gépek általában ide tartoznak.

Párhuzamos gép modellek

PRAM modell

• PRAM: Parallel Random Access Machine

• PU: Processing Unit

Figyelem

A PU-t magyarul számítási egység-nek fordíthatjuk. Az egyszerűség kedvéért tekinthetjük ezeket processzoroknak vagy szálaknak. Mivel egyelőre nem kötődünk fizikai megvalósításhoz, ezért csak azt feltételezzük, hogy szekvenciális végrehajtásra alkalmas.

Egy absztrakt modellről van szó.

• A PU-k száma tetszőleges sok lehet.

• A memória méretére vonatkozóan nem ad meg limitet.

• Minden PU szimultán hozzá tud férni a memóriához.

(Ezek a feltételezések valós gépek esetén sajnos nem állnak fenn.)

A modellt a memóriához való hozzáférés alapján tovább szokták pontosítani.

CREW: Concurrent Read - Exclusive Write

• Egy adott memóriacellát minden PU tud olvasni tetszőleges időpontban, viszont

• egyszerre csak egy tudja írni.

CRCW: Concurrent Read - Concurrent Write

Feltételezi, hogy mindegyik PU egyszerre tud olvasni és írni is egy adott memória cellát. Ez az érték beállítása szempontjából problémás lehet, ezért erre vonatkozóan külön megközelítések vannak.

• tetszőleges mód: Nincs definiálva, hogy konkurrens hozzáférés esetén mi fog történni. Egy nem-determinisztikus gépet kapunk így.

• konzisztens mód: Mindegyik PU-nak ugyanazt az értéket lehet csak beírnia.

• prioritásos mód: A PU-k között van egy sorrend, amely alapján mindig eldönthető, hogy ütközés esetén melyiknek az értéke kerül be a memóriába.

• fúziós mód: Egyidejű írás esetén egy aggregálást hajt végre. A művelet kommutatív és asszociatív kell, hogy legyen, mint például a minimum, maximum, AND, OR, szummázás műveletek.

EREW: Exclusive Read - Exclusive Write

• Ez a leginkább realisztikus modell.

• Egyidejűleg egy cellához csak egy PU férhet hozzá.

\(\rhd\) Melyik kombináció maradt ki? Mi lehet annak az oka?

Számítási költség és hatékonyság

Vezessük be a következő jelöléseket!

• \(P\): a megoldandó probléma

• \(n\): a probléma mérete

• \(T_{\text{seq}}(n)\): számítási idő szekvenciális végrehajtás esetén

• \(T_{\text{par}}(p, n)\): számítási idő párhuzamos végrehajtás esetén \(p\) darab PU-val.

Költség (Cost)

\[C_p(n) = p \cdot T_{\text{par}}(p, n)\]

Munka (Work)

\(W_p(n)\): Az összes PU-n elvégzett műveletek összege.

• Ideális esetben a munka és a költség meg kellene, hogy egyezzen.

• A költség akkor lesz minimális, hogy ha minden PU hasznosan tölti az időt (nem várakozik).

• Szekvenciális esetben a kettő megegyezik. (Ez tekinthető a \(p = 1\) esetnek is.)

Gyorsítás (Speed-Up)

\[S_p(n) = \dfrac{T_{\text{seq}}(n)}{T_{\text{par}}(p, n)}\]

• Ideális esetben a párhuzamos végrehajtás gyorsabb, mint a szekvenciális, így egy 1-nél nagyobb értéket kapunk.

• A mennyiséget gyakran százalékos formában használják.

• Tétel: \(p\)-nél nagyobb gyorsítás nem érhető el!

Hatékonyság (Efficiency)

\[E_p(n) = \dfrac{S_p(n)}{p} = \dfrac{T_{\text{seq}}(n)}{p \cdot T_{\text{par}}(p, n)}\]

\(\rhd\) A definiált értékekből hogyan lehetne egyszerűen kiszámítani a hatékonyságot?

\(\rhd\) Milyen intervallumon változhat a hatékonyság értéke?

A hatékonyság romlásának lehetséges okai:

• Kiegyenlítetlenség

• Kommunikációs költség, adminisztrációs költség (overhead)

\(\rhd\) Miért lehet fontos a futási idő és a gyorsítás mellett a hatékonysággal is foglalkozni?

Számítási példa

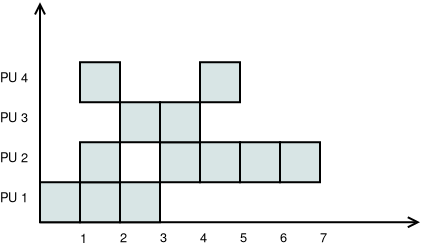
Számítsuk ki a költség, munka, gyorsítás és hatékonyság értékeket!

Komplexitás mérése

\(\rhd\) Milyen ordo szimbólumok vannak, és mit jelentenek?

\(f(n) = \mathcal{O}(g(n))\), ha \(\exists c > 0\) és \(n_0 > 0\), hogy ha \(n \geq n_0\), akkor \(0 \leq f(n) \leq c \cdot g(n)\).

\(f(n) = \Omega(g(n))\), ha \(\exists c > 0\) és \(n_0 > 0\), hogy ha \(n \geq n_0\), akkor \(0 \leq c \cdot g(n) \leq f(n)\).

\(f(n) = \Theta(g(n))\), ha \(\exists c_1, c_2 > 0\) és \(n_0 > 0\), hogy ha \(n \geq n_0\), akkor \(0 \leq c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)\).

\(f(n) = \mathcal{o}(g(n))\), ha \(\forall c > 0\)-ra \(\exists n_0 > 0\), hogy ha \(n \geq n_0\), akkor \(0 \leq f(n) < c \cdot g(n)\).

\(f(n) = \omega(g(n))\), ha \(\forall c > 0\)-ra \(\exists n_0 > 0\), hogy ha \(n \geq n_0\), akkor \(0 \leq c \cdot g(n) < f(n)\).

\(\rhd\) Egy-egy példán ábrázoljuk, hogy az adott szimbólumok milyen kapcsolatot adnak meg a bonyolultságot leíró függvény, és a segédfüggvények között!

Párhuzamos komplexitás:

\[T_{\text{par}}(p, n) = \min(\max_i t_i), \quad 1 \leq i \leq p\]

\(\rhd\) Próbáljuk meg ábrával szemléltetni az összefüggést?

\(\rhd\) A kifejezésben hogy jelenik meg a problémaméret?

Megjegyzés

A \(T_{\text{seq}}\) és a \(T_{\text{par}}\) esetében is feltételezzük, hogy a legjobb elérhető algoritmust használjuk, és a futási idő szempontjából a legrosszabb bemenet számítási idejét vesszük.

A párhuzamos végrehajtásból eredő gyorsítás jellemzése

• Szublineáris gyorsítás: \(S_p = o(p)\)

• Lineáris gyorsítás: \(S_p = \Theta(p)\)

• Szuperlineáris gyorsítás: \(S_p = \omega(p)\)

Munkahatékony algoritmus

Egy párhuzamos algoritmus a soros algoritmusra nézve munkahatékony, hogy ha létezik olyan \(k\) érték, hogy

\[\dfrac{p \cdot T_{\text{par}}(n, p)}{T_{\text{seq}}(n)} = \mathcal{O}(\text{lg}^k n).\]

• Egy párhuzamos algoritmus csak akkor munkahatékony, hogy ha legalább lineáris a gyorsítása.

• Egy munkahatékony párhuzamos algoritmus hatékonysága \(\Theta(1)\).

Munkaoptimális algoritmus

Egy párhuzamos algoritmus a soros algoritmusra nézve munkaoptimális, hogy ha

\[\dfrac{p \cdot T_{\text{par}}(n, p)}{T_{\text{seq}}(n)} = \mathcal{O}(1).\]

Szimuláció kevesebb PU-val

Tegyük fel, hogy egy \(\mathcal{A}\) algoritmust egy \(p\) darab PU-val rendelkező PRAM gépen \(t\) idő alatt oldunk meg. Ugyanezen számítás egy azonos típusú gépen \(p' \leq p\) számú PU-val szimulálható \(\mathcal{O}\left(t \cdot \dfrac{p}{p'}\right)\) idő alatt.

A \(p'\) számú PU-val rendelkező gép költsége legfeljebb duplája lesz a \(p\) számú PU-val rendelkezőjének.

Bizonyítás

Az \(\mathcal{A}\) algoritmus minden lépése \(\left\lceil\dfrac{p}{p'}\right\rceil\) időegység alatt szimulálható a \(p'\) PU-val a konkurrens részek szekvenciálissá tételével.

Mivel az eredeti számítás \(t\) időegységig tartott, ezért a szimulált \(t \cdot \left\lceil\dfrac{p}{p'}\right\rceil\) lesz, amelyből megkapjuk, hogy az időbonyolultság \(\mathcal{O}\left(t \cdot \dfrac{p}{p'}\right)\).

Számítsuk ki a \(p'\) PU-val rendelkező gép költségét! Jelölje \(t'\) ennek a gépnek a számítási idejét!

\[C_{p'}(n) = p' \cdot t' \leq p' \cdot t \cdot \left\lceil\dfrac{p}{p'}\right\rceil \leq p' \cdot t \cdot \left(\dfrac{p}{p'} + 1\right) = p \cdot t \left(1 + \dfrac{p'}{p}\right) \leq p \cdot t \cdot 2 = 2 \cdot C_p(n)\]

Így tehát azt kapjuk, hogy

\[C_{p'}(n) \leq 2 \cdot C_p(n). \quad \square\]

Brent tétele

Tegyük fel, hogy egy \(\mathcal{A}\) algoritmus összesen \(m\) művelet végrehajtásával jár, és \(t\) ideig tart. Ugyanezen típusú gépen, \(p\) darab PU-val \(\mathcal{O}\left(\dfrac{m}{p} + t\right)\) idő alatt szimulálható.

Bizonyítás

Tegyük fel, hogy az \(\mathcal{A}\) algoritmus az \(i\)-edik lépésben \(m(i)\) műveletet hajt végre. Az összes lépést elvégezve ez visszaadja \(m\)-et:

\[m = \displaystyle \sum_{i=1}^{t} m(i).\]

Az \(i\)-edik lépés szimulálható \(\left\lceil\dfrac{m(i)}{p}\right\rceil\) időegység alatt, amelyre fennáll, hogy

\[\left\lceil\dfrac{m(i)}{p}\right\rceil \leq \dfrac{m(i)}{p} + 1.\]

Könnyen látható, hogy

\[\displaystyle \sum_{i=1}^{t} \left(\dfrac{m(i)}{p} + 1\right) = \dfrac{m}{p} + t,\]

amelyből adódik a tétel állítása. \(\square\)

Amdahl törvénye

• Gene Amdahl, 1967.

• Azt mutatja meg, hogy egy program esetében a párhuzamosítható részek arányát ismerve ideális esetben mennyi lesz a gyorsítás (speedup) értéke.

• A probléma méretét rögzítettnek tekinti.

• Egy felső becslésről van szó.

Használjuk a következő jelöléseket!

• \(p\): a számítási egységek száma

• \(f\): a program egészére nézve a párhuzamosítható részek aránya

\[S_p = \dfrac{1}{(1 - f) + \dfrac{f}{p}}\]

Figyelem

A törvény elméleti felső korlátot ad!

\[\lim_{p \rightarrow \infty} S_p = \dfrac{1}{1 - f}\]

\(\rhd\) Vizsgáljuk meg az \(f \rightarrow 0\) és az \(f \rightarrow 1\) eseteket!

\(\rhd\) Mennyinek kell lennie legalább a párhuzamosítható részek arányának, hogy ha legalább 10-szeres gyorsítást szeretnénk elérni?

\(\rhd\) Mennyi lesz ez 1000-szeres gyorsítás esetében?

\(\rhd\) Tegyük fel, hogy egy algoritmusban a párhuzamosítható részek aránya 80%. Legalább mennyi számítási egységre van szükségünk, hogy 4-szeres gyorsítást el tudjunk érni?

\(\rhd\) Ábrázoljuk az összefüggést!

Gustafson-Barsis törvény

• John L. Gustafson, Edwin H. Barsis, 1988.

• Tetszőlegesen nagy méretű problémát feltételez.

Használjuk a következő jelöléseket!

• \(p\): a számítási egységek száma

• \(f\): a program egészére nézve a párhuzamosítható részek aránya

\[S_p = (1 - f) + p \cdot f\]

\(\rhd\) Tegyük fel, hogy van egy 64 számítási egységet tartalmazó számítógépünk! Feltételezve, hogy tetszőlegesen sok időnk lehet, maximálisan mennyi lehet a gyorsítás mértéke, hogy ha a program 90%-a párhuzamosítható?

\(\rhd\) Tegyük fel, hogy egy program 60%-a párhuzamosítható! A Gustafson-Barsis törvény alapján legalább mennyi számítási egységre van szükségünk, hogy 40-szeres gyorsítást tudjunk elérni?

\(\rhd\) Ábrázoljuk az összefüggést!

Párhuzamosság ábrázolása

\(\rhd\) Adjunk példákat, hogy hol szoktak ilyen ábrázolási módokat használni!

Gantt diagram

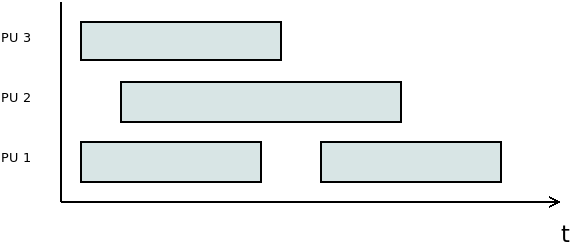
Szekvencia diagram

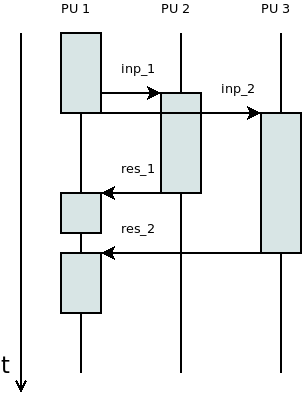
Problématér felosztása

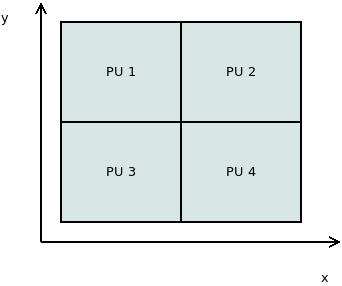
Hívási fa

• Elsősorban nem párhuzamos végrehajtást szokás vele ábrázolni.

• Az „Osszd meg és uralkodj!” elv szerint a problématér felosztása (főleg rekurzív esetekben) nagyon szépen ábrázolható vele.

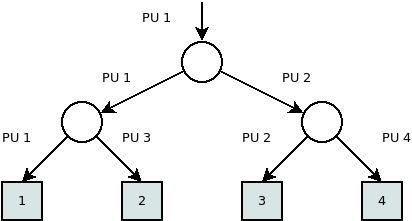
Aggregáció, redukció

Legyen adott egy \(\Sigma\) alaphalmaz. Definiáljuk rajta a \(\oplus\) bináris, asszociatív operátort. (A \(\Sigma\)-ról tudjuk, hogy zárt a műveletre nézve.)

Tegyük fel, hogy adott egy \(X\) bemeneti sorozat, és egy \(z\) eredmény értéket keresünk:

\[z = \bigoplus_{i=1}^{n} x_i\]

\(\rhd\) Adjunk példát ilyen műveletekre!

\(\rhd\) Adjuk meg a szekvenciális algoritmust és annak időigényét!

\(\rhd\) Vizsgáljuk meg a szóbajöhető iteratív és rekurzív algoritmusokat!

\(\rhd\) Adjunk olyan párhuzamos algoritmust, amellyel csökkenthető a számítási idő!

Prefix számítás

Legyen adott egy \(\Sigma\) alaphalmaz. Definiáljuk rajta a \(\oplus\) bináris, asszociatív operátort. (A \(\Sigma\)-ról tudjuk, hogy zárt a műveletre nézve.)

Tekintsünk egy \(X = [x_1, x_2, \ldots, x_n]\) sorozatot.

Az \(x_1 \oplus \cdots \oplus x_k\) elemeket prefixeknek nevezzük. A számítás célja ezek meghatározása.

CREW_PREFIX algoritmus

CREW PRAM modellt használ. A problémát rekurzívan oldja meg.

• Egy elem esetén az elem maga a prefix.

• Több elem esetén a tömböt 2 részre osztja. Rekurzívan végrehajta rajta a prefix számítást, majd a tömb második felének minden eleméhez hozzáadja a tömb első felének utolsó elemét.

Az algoritmus időigénye a következőképpen számítható.

\[T(n) = T\left(\dfrac{n}{2}\right) + \mathcal{O}(1), \quad T(1) = 1 \quad \Rightarrow \quad T(n) = \mathcal{O}(\text{log}_2(n))\]

• A CREW-PREFIX algoritmus nem munkaoptimális, mivel \(\Theta(n \cdot \text{log}_2 n)\) munkát végez, míg van olyan szekvenciális algoritmus, amelynél ez \(\mathcal{O}(n)\).

EREW_PREFIX algoritmus

EREW PRAM modellt használ.

\[\begin{split}\begin{align*} &\text{EREW_PREFIX}(@X, @Y) \\ &\text{// Input}: X, n \text{ elemű sorozat.} \\ &\text{// Output}: Y, n \text{ elemű sorozat.} \\ &y_1 \leftarrow x_1 \\ &\text{PARALLEL FOR } i \leftarrow 2 \text{ TO } n \text{ DO} \\ &\quad y_i \leftarrow x_{i-1} \oplus x_i \\ &k \leftarrow 2 \\ &\text{WHILE } k < n \text{ DO} \\ &\quad \text{PARALLEL FOR } i \leftarrow k + 1 \text{ TO } n \text{ DO} \\ &\quad \quad y_i \leftarrow y_{i - k} \oplus y_i \\ &\quad k \leftarrow 2 \cdot k \\ &\text{RETURN}(Y) \\ \end{align*}\end{split}\]

Az EREW_PREFIX algoritmus időigénye \(n\) processzoron \(\Theta(\text{log}_2(n))\).

OPTIMAL_PREFIX algoritmus

CREW PRAM számítási modell. Tegyük fel, hogy \(p = \dfrac{n}{\text{log}_2(n)}\) processzort használunk.

• Osszuk fel az \(X\) bemeneti sorozatot \(\dfrac{n}{\text{log}_2(n)}\) részre, és oldjuk meg rajtuk szekvenciálisan a prefix számítási problémát! Az eredmény kerüljön az \(Y\) tömbbe!

• Gyűjtsük ki a résztömbök utolsó elemeit egy \(Z\) segédtömbbe!

• A CREW_PREFIX algoritmust hajtsuk végre a \(Z\) tömbön, és az eredmény kerüljön egy \(W\) tömbbe!

• Az \(\dfrac{n}{\text{log}_2(n)}\) részre bontott \(Y\) tömb elemeihez adjuk hozzá a \(W\) tömbben lévő megfelelő értéket! (A \(j\)-edik résztömb minden eleméhez a \(w_{j-1}\) értéket, ahol \(1 < j \leq \dfrac{n}{\text{log}_2(n)}\).)

Az algoritmus mindhárom lépése \(\Theta(\text{log}(n))\) ideig tart, így a teljes számítás is \(\Theta(\text{log}(n))\) időbonyolultságú.

Az Optimális PREFIX számítás munkaoptimális.

Példa

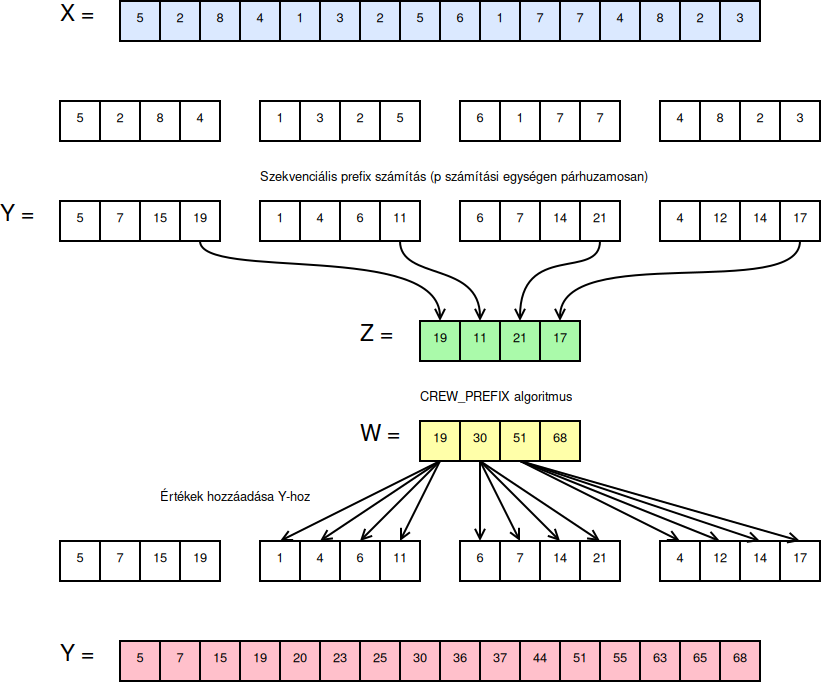
Kérdések

Moore törvény

1. Feltételezzük, hogy a számítási egységek száma 2 évente megkétszereződik. Tegyük fel, hogy 1965-ben ez 100 volt. Várhatóan mennyi lesz 1990-ben?

2. Feltételezzük, hogy a tranzisztorok száma 2 évente duplázódik. Hogy ha 1980-ban ez a szám 20000, akkor mennyi volt 1970-ben?

3. Tegyük fel, hogy a számítási kapacitás 18 havonta megduplázódik. Tekintsük ezt 1970-ben 1000-nek. Hogyan írható fel az a függvény, amely az év függvényében megadja a tendencia szerint várható számítási kapacitást!

Komplexitás becslése

1. Lássa be, hogy a \(T(n) = (n + 1)(n + 5) - 4\) függvény növekedési rendje \(\mathcal{O}(n^2)\)!

2. Lássa be, hogy a \(T(n) = n^2 + 2\) függvény növekedési rendje \(\mathcal{O}(n^3)\)!

3. Lássa be, hogy a \(T(n) = 2^{n + 3}\) függvény növekedési rendje \(\mathcal{O}(e^n)\)!

4. Lássa be, hogy a \(T(n) = 3 \cdot x^2\) függvény növekedési rendje \(\mathcal{O}(2^x)\)!

5. Lássa be, hogy a \(T(n) = 3 \cdot \text{log}_{4}(x)\) függvény növekedési rendje \(\mathcal{O}(\text{ln}x)\)!

Amdahl törvénye

1. Mennyinek kell lennie legalább a párhuzamosítható részek arányának, hogy ha legalább 12-szeres gyorsítást szeretnénk elérni?

2. Tegyük fel, hogy egy algoritmusban a párhuzamosítható részek aránya 87%. Legalább mennyi számítási egységre van szükségünk, hogy 7-szeres gyorsítást el tudjunk érni?

3. Egy programban a párhuzamosítható részek aránya 70%. Hogy ha 16 számításokat végző egységünk van, akkor mekkora az elérhető maximális gyorsítás?

4. Tudjuk, hogy 2.5-szörös gyorsítást tudunk elérni maximálisan egy adott program párhuzamos futtatásakor. A program 80%-a párhuzamosítható. Mennyi számítási egységünk van?

Technikai tudnivalók

• A feladatok megoldásához a D meghajtón hozzon létre egy saját mappát!

• Töltse le a fejlesztőkörnyezetet a következő címről: c_sdk_220203.zip

• Ezt célszerű úgy kitömöríteni, hogy a MinGW jegyzék közvetlenül a saját mappában legyen.

• Ebbe célszerű klónozni az me-courses nevű repozitory-t, illetve a fejlesztéshez használt saját repository-t is.

• Az elkészített kódok fordításához indítsa el a shell.bat batch fájlt!

• Egy forrásfájlból álló C programok esetében az alábbi paranccsal tudja elvégezni a fordítást:

gcc program_neve.c -o program_neve.exe

• A program futtatásához írja be a parancssorba, hogy program_neve vagy pedig, hogy program_neve.exe.

Feladatok

1. Nézze át a git alapvető műveleteit!

   • Klónozza a https://gitlab.com/imre-piller/me-courses.git címen lévő repository-t!

   • Kérdezze le a repository-hoz tartozó branch-eket!

   • Váltson át a parallel nevű branch-re!

2. Írjon egy programot, amelyik egész értékeket ír ki pontosan 8 karakter hosszan (jobbra igazítva)! Oldja meg úgy, hogy szóközökkel, továbbá hogy 0 értékekkel van kitöltve a szám eleje (amennyiben szükséges kitölteni)!

3. Készítsen példát a sleep függvény használatára!

4. Generáljon véletlenszámot az \([500, 1000]\) intervallumon! (Oldja meg lebegőpontos és egész számok esetére is!)

5. Készítsen egy programot, amely a bemeneti argumentumként kapott két egész szám között (zárt intervallumon) generál egy szintén egész véletlen számot! Ellenőrízze az argumentumok számát, és jelezzen hibát, amennyiben nem megfelelőek!

6. Írjon egy programot, amelyik 2 véletlenszerűen meghatározott pozitív egész szám értékét számoltatja ki a felhasználóval, és a szabványos bemeneten várja az eredményt! Ellenőrízze, hogy helyes az érték, és írja ki, hogy mennyi ideig tartott (másodpercben) a felhasználónak a számítás!

7. Definiáljon egy függvényt, amely az \([1, n]\) intervallumon meghatározza a prímszámok számát! Mérje le a futási időt az \(n = 1000, 2000, 3000, \ldots, 20000\) értékeknél, és jelenítse meg grafikonon a kapott eredményeket (például Excel-el)!

8. Írjon egy programot, amely egy tömbben lévő értékeket kiírja egy fájlba!

   • A műveletet szervezze ki egy külön függvénybe!

   • Készítse el int, long és float típusok esetére is (külön függvényekkel)!

   • Kérdezze le, hogy az adott útvonalon lévő fájlnak mekkora a mérete!

   • Készítse el a függvényeket az adatok visszaolvasásához!

9. Készítsen egy programot, amelyik a paraméterként vár egy fájlnevet és egy elemszámot (mint egész értéket).

   • Ezek alapján hozza létre a program az adott fájlt véletlenszerű értékekkel kitöltve, a megfelelő elemszámmal!

   • Mérje le a véletlenszámok generálásának sebességét az elemszám függvényében!

   • Mérje le a fájl mentésének idejét az elemszám függvényében!

   • Gyűjtse össze a kapott mérési adatokat táblázatba, és ábrázolja őket grafikonon!