7. Előadás - Numerikus módszerek

Skaláris szorzat

Tegyük fel, hogy adott egy \(a \in \mathbb{R}^n\) és egy \(b \in \mathbb{R}^n\) vektor. Ezek skaláris szorzata a következőképpen számítható ki:

\[s = \displaystyle\sum_{i=1}^n a_i \cdot b_i.\]

A számítás párhuzamos végrehajtásához

  • a szorzások időben egyszerre, egymástól függetlenül is elvégezhetők, majd

  • a kapott \(n\) számú elem összeadására van szükség.

Időbonyolultság

  • Az \(s\) kiszámításához \(n\) darab szorzásra és \(n - 1\) összeadásra van szükség.

  • Szekvenciális esetben \(T(n) = \Theta(n)\).

  • Párhuzamos esetben feltehetjük, hogy minden szorzás időben egyszerre végződik el (1 konstans lépés), az összegzés pedig logaritmikus időben, vagyis \(T(n) = \Theta(1 + \log_2 n)\).

Munka

Tegyük fel, hogy a szorzás és az összeadás számítási idejét egyenlőnek tekintjük! Szekvenciális esetben ekkor:

\[W(n) = 2n - 1.\]

(Párhuzamos esetben szintén ezt kapjuk.)

Költség

A költség attól függően változhat, hogy a gyorsításra, vagy a hatékonyságra optimalizálunk.

A gyorsítás esetében \(p = n\) processzorra van szükségünk.

  • Az első lépésben minden processzoron 1-1 darab szorzás műveletet hajtunk végre.

  • \(\log_2 n\) számú további lépésre van szükség.

  • Ezen további lépésekben \(n - 1\) összeadás történik.

Összességében azt kapjuk, hogy:

\[C_p(n) = n \cdot (1 + \log_2 n), \quad S_p(n) = \dfrac{2n - 1}{1 + \log_2 n}, \quad E_p(n) = \dfrac{2n - 1}{n \cdot (1 + \log_2 n)}.\]

Ábrázolva az eredményeket \([1, 1000]\) méretű bemenetekre:

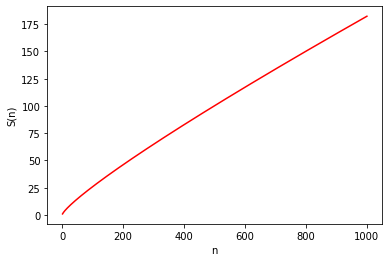
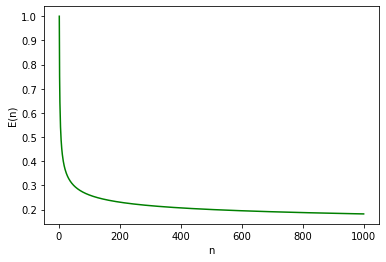
../../_images/scalar_sn_1.png ../../_images/scalar_en_1.png

Tegyük fel, hogy célként a hatékonyság maximalizálását tűzzük ki!

  • Az \([1, n]\) intervallumot feloszthatjuk \(p\) részre.

  • Mindegyik részhez nagyságrendileg \(\dfrac{n}{p}\) szorzás, és 1-gyel kevesebb összeadás fog tartozni.

  • További \(p - 1\) számú összeadásra van szükség, amely már \(\log_2 p\) lépésben elvégezhető.

Összességében azt kapjuk, hogy:

\[\begin{split}\begin{align*} &C_p(n) = p \cdot \left(2 \cdot \dfrac{n}{p} - 1 + \log_2 p\right), \\ &S_p(n) = \dfrac{2n - 1}{2 \cdot \dfrac{n}{p} - 1 + \log_2 p}, \\ &E_p(n) = \dfrac{2n - 1}{p \cdot \left(2 \cdot \dfrac{n}{p} - 1 + \log_2 p\right)}. \end{align*}\end{split}\]

A felírás természetesen egyszerűsíthető, hogy ha a

\[T_p(n) = 2 \cdot \dfrac{n}{p} - 1 + \log_2 p\]

formában adjuk meg a számítási lépések számát a párhuzamos végrehajtás esetében.

Ábrázolva az eredményeket \([1, 1000]\) méretű bemenetekre, \(p = 4\) esetén:

../../_images/scalar_sn_2.png ../../_images/scalar_en_2.png

Mátrix szorzás

Legyen adott három mátrix:

  • \(A \in \mathbb{R}^{n \times m}\),

  • \(B \in \mathbb{R}^{m \times r}\),

  • \(C \in \mathbb{R}^{n \times r}\).

Az \(A\) és \(B\) mátrixból a \(C\) mátrixot, mint szorzatot a következőképpen kapjuk:

\[c_{ij} = \displaystyle\sum_{k=1}^m a_{ik} \cdot b_{kj}.\]

Jól látható, hogy

  • a szorzat mátrix elemei időben egyszerre, egymástól függetlenül számolhatók, és

  • mivel a \(C\) minden eleme egy skaláris szorzat, így azon skaláris szorzatok számítása is megoldható párhuzamosítva.

Munka

  • A teljes számítás elvégzéséhez \(n \cdot r\) skaláris szorzatot kell kiszámítani.

  • Minden szorzat \(m\) elemű vektorok szorzását jelenti.

  • \(m\) elemű vektorokon \(m\) szorzás és \(m - 1\) összeadás elvégzésére van szükség.

  • Feltételezhetjük, hogy az összeadás és a szorzás műveletideje azonos. (Praktikusan egy processzor ciklus alatt elvégezhető. Ez természetesen nem minden rendszerben szükségszerű feltételezés.)

\[W(n, m, r) = n \cdot r \cdot (m + m - 1)\]

Számítási idő

Szekvenciális esetben \(T(n, m, r) = W(n, m, r)\).

  • Párhuzamosítás esetén elvileg minden \(c_{ij}\) elem számítása időben egyszerre történhet.

  • Egy \(c_{ij}\) elem számításához elegendő \(T(m) = \Theta (1 + \log_2 m)\) számítási lépést elvégezni.

Gyorsítás

Az előzőek alapján azt kapjuk, hogy

\[S_p(n, m, r) = \dfrac{n \cdot r \cdot (m + m - 1)}{1 + \log_2 m}.\]

Vizsgáljuk meg a gyorsítást négyzetes mátrixok esetében (vagyis amikor \(n = m = r\))!

\[S_p(n) = \dfrac{2n^3 - n^2}{1 + \log_2 n}.\]
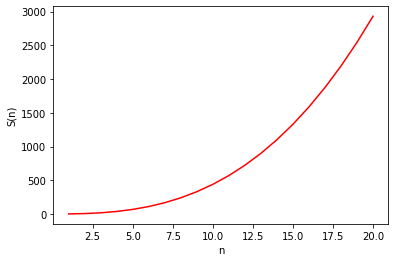
../../_images/matrix_speedup.png

Ez esetben feltételeztük, hogy tetszőleges nagy lehet a \(p\) értéke. Ahhoz, hogy ez valóban így adódjon

\[p = n \cdot r \cdot \dfrac{m}{2}\]

számítási egységre lenne szükségünk.

  • A skaláris szorzat számítása kapcsán láthattuk, hogy adható hatékony párhuzamos algoritmus a számítására.

  • A \(c_{ij}\) értékek számítási egységek közötti elosztása szintén hatékonyan elvégezhető.

  • \(p\) függvényében adható tehát olyan algoritmus (problématér felosztás), amelyre a hatékonyság a probléma méretének növelésével 1-hez fog tartani.

Lineáris egyenletrendszerek megoldása

Tekintsük az \(Ax = b\) egyenletrendszert, ahol

  • \(A \in \mathbb{R}^{n \times n}\) együtthatómátrix,

  • \(b \in \mathbb{R}^n\) vektor,

  • \(x \in \mathbb{R}^n\) ismeretleneket tartalmazó vektor.

A lineáris egyenletrendszer megoldásához Gauss eliminációt használhatunk.

Felső háromszögmátrix számítása

\[\begin{split} \begin{align*} &\text{CALC_TRIANGLE}(@A, @b) \\ &\text{// Input}: A \in \mathrm{R}^{n \times n} \\ &//\quad\quad\quad\, b \in \mathrm{R}^n \\ &\text{// Output}: A \in \mathrm{R}^{n \times n} \\ &//\quad\quad\quad\, b \in \mathrm{R}^n \\ &\text{FOR }k \leftarrow 1\text{ TO }n - 1\text{ DO}\\ &\quad\text{FOR }i \leftarrow k + 1\text{ TO }n\text{ DO}\\ &\quad\quad a_{ik} \leftarrow \dfrac{a_{ik}}{a_{kk}}\\ &\quad\quad \text{FOR }j \leftarrow k + 1\text{ TO }n\text{ DO}\\ &\quad\quad\quad a_{ij} \leftarrow a_{ij} - a_{ik} \cdot a_{kj}\\ &\quad\quad b_i \leftarrow b_i - a_{ik} \cdot b_k\\ &\text{RETURN}(A, b) \\ \end{align*}\end{split}\]

Visszahelyettesítés

\[\begin{split} \begin{align*} &\text{BACK_SUBSTITUTE}(@A, @b, @x) \\ &\text{// Input}: A \in \mathrm{R}^{n \times n} \\ &//\quad\quad\quad\, b \in \mathrm{R}^n \\ &\text{// Output}: x \in \mathrm{R}^n \\ &\text{FOR }i \leftarrow n\text{ DOWNTO }1\text{ DO}\\ &\quad x_i \leftarrow b_i\\ &\quad \text{FOR }j \leftarrow i + 1\text{ TO }n\text{ DO}\\ &\quad\quad x_i \leftarrow x_i - a_{ij} \cdot x_j\\ &\quad x_i \leftarrow \dfrac{x_i}{a_{ii}}\\ &\text{RETURN}(x) \\ \end{align*}\end{split}\]

Figyelem

A lineáris egyenletrendszerek megoldásának ez az egyik legegyszerűbb esete. A gyakorlatban érdemes például főelemkiválasztást is használni hozzá!

Párhuzamosítás

A háromszögmátrix számítása esetében az \(i\)-hez tartozó sorok párhuzamosan kiszámíthatók.

A visszahelyettesítés esetében a \(j\)-hez tartozó ciklus szintén párhuzamosítható.

Bizonyos elemszám alatt a párhuzamosításnak már nincs értelme a gyakorlatban, így azt szekvenciális formában érdemes számolni.

Determináns számítása

  • A Gauss eliminációt követően a felsőháromszög mátrix átlójában lévő elemeinek szorzatából számítható.

  • A szorzat számítása logaritmikus idő alatt elvégezhető.

Interpoláció

Legyenek adottak \(x_1, x_2, \ldots, x_n \in \mathbb{R}\) pontok, és hozzá tartozó \(y_1, y_2, \ldots, y_n \in \mathbb{R}\) értékek. A célunk az, hogy megadjunk egy olyan \(f: \mathbb{R} \rightarrow \mathbb{R}\) függvényt, amelyre teljesül, hogy \(f(x_i) = y_i\) bármilyen \(1 \leq i \leq n\) érték esetén.

Az egyszerűség kedvéért feltételezzük, hogy \(i < j \Rightarrow x_i < x_j\).

Lineáris interpoláció

\[f(x) = y_i + \dfrac{x - x_i}{x_{i+1} - x_i} \cdot (y_{i+1} - y_i),\]

ahol \(x \in [x_i, x_{i+1}]\).

Hogy ha egyetlen \(y\) értéket szeretnénk meghatározni, akkor a problémát alapvetően az \(i\) érték számítása jelenti.

  • Az \(x_i\) értékek rendezettségét kihasználva az intervallum keresése logaritmikus időben elvégezhető.

  • Minden részintervallumhoz egy számítási egységet rendelve konstans idő is elérhető. (Itt problémát jelenthet, hogy az adminisztratív költség nagyobb, mint maga az elvégzendő számítás.)

  • Egyenközű felbontást feltételezve az index közvetlenül számítható az \(x\) értékből.

Tegyük fel, hogy több helyen szeretnénk meghatározni az interpolációs függvény értékét!

  • Feltételezve, hogy a behelyettesítendő \(x\) értékek sorrendben következnek, nem szükséges, csak az első esetben meghatározni az intervallum indexét, majd minden lépésben figyelni, hogy még az adott intervallumban vagyunk-e.

  • A feladat felbontható \(p\) részre, amellyel így közel \(p\)-szeres gyorsítás érhető el.

Lagrange interpoláció

\[L(x) = \displaystyle\sum_{i=1}^{n} y_i \cdot \mathcal{l}_i(x),\]

ahol

\[\mathcal{l}_i(x) = \displaystyle\prod_{k=1,k\neq i}^{n} \dfrac{x - x_k}{x_i - x_k}.\]

  • A számítás szekvenciális esetben \(T(n) = \Theta(n^2)\) idejű.

  • A szumma tagjai és a produktum tényezői is időben egyszerre számolhatók.

Numerikus integrálás

Az integrál közelítéséről számos módszer rendelkezésre áll. Ezek közül a Trapéz módszer a következő formában ad közelítést egy \([a, b)\) rész intervallumra:

\[\int_{a}^{b} f(x) \mathrm{d}x \approx \dfrac{b - a}{2} (f(a) + f(b))\]

A párhuzamosítást egyszerűen a részintervallumokra bontással oldhatjuk meg.

  • Ekvidisztáns intervallum felbontást alkalmazhatunk.

  • Az egyes intervallumokon a számítást külön-külön elvégezhetjük.

  • A kapott eredményeket párhuzamos algoritmus segítségével összegezhetjük.

\(\rhd\) Hogyan rendelhetők a szálakhoz az intervallumok?

\(\rhd\) Párhuzamos algoritmussal végezve az integrál közelítését mennyi lesz a \(W_p, C_p, S_p, E_p\)?

\(\rhd\) Hogyan adható az intervallum szélességére vonatkozó maximális értékkel a probléma megoldására rekurzív algoritmus?

Tegyük fel, hogy a közelítés pontosságát szeretnénk a rekurzív változat megállási feltételeként használni.

  • Jelölje \(T(a, b)\) az \([a, b)\) intervallumra vonatkozó közelítés értékét!

  • Használjunk egy \(\varepsilon \in \mathbb{R}\) hibaértéket!

  • Az intervallumok közepét számítsuk ki a \(c = \dfrac{a + b}{2}\) formában!

  • A leállási feltételünk ekkor

\[|T(a, b) - (T(a, c) + T(c, b))| < \varepsilon.\]

\(\rhd\) Milyen esetben adódhatnak problémák ezzel a számítási móddal?

Kérdések

  • Két \(n\) elemű vektor skaláris szorzatának a számításakor teljesülhet-e, hogy az időbonyolultság \(T(n) = \mathcal{O}(\log_2 n)\)? (Lássa is be!)

  • Mennyi az elérhető maximális gyorsítás (elvi szinten) az \(A \in \mathbb{R}^{n \times m}\) és \(B \in \mathbb{R}^{m \times r}\) mátrixok szorzása esetében (CREW modellt feltételezve)?

  • Mennyi összeadás és mennyi szorzás művelet elvégzésére van szükség két \(k \times k\) méretű mátrix összeszorzása során?

  • Tegyük fel, hogy adott egy \(A \in \mathbb{R}^{10 \times 30}\) és egy \(B \in \mathbb{R}^{30 \times 20}\) mátrix. Mennyi összeadás és szorzás elvégzésére van szükség a szorzatuk kiszámításához? Mennyi az elméleti minimum számítási lépés párhuzamos végrehajtás esetén? Mennyi az elérhető maximális gyorsítás?

Feladatok

Mátrixok

  1. Készítsen párhuzamos programokat, amelyekkel megvizsgálható, hogy egy mátrix

    • egység mátrix-e,

    • diagonális-e,

    • szimmetrikus-e.

  2. Készítsen egy olyan programot, amely megvizsgálja, hogy egy mátrixra elemeire teljesül-e bizonyos tulajdonság.

    • A tulajdonság megadásához definiáljon egy függvényt, amely a mátrix adott elemének értékétől, és a hozzá tartozó indexektől függ.

  3. Vizsgáljuk meg az 1-es, 2-es és a végtelen normák számítási módját!

    • Készítsünk ezekhez párhuzamos algoritmust!

    • Számítsuk ki az elvért időbonyolultságot!

    • Implementáljuk POSIX szálak és/vagy OpenMP segítségével!

    • Végezzük méréseket, összegezzük, ábrázoljuk és értelmezzük a kapott eredményeket!

Skaláris szorzat

  • Az elméleti számításokba nem került figyelembevételre a probléma felbontásának a költsége. Végezzünk méréseket arra vonatkozóan, hogy különböző \(n\) és \(p\) értékek esetében milyen számítási időkkel, gyorsítással és hatékonysággal számolhatunk a gyakorlatban!

Interpoláció

  • Vizsgáljuk meg, hogy Lagrange interpoláció esetében mekkora az a problémaméret, amelytől kezdve már megéri a polinom értékét párhuzamosan számolni!

Numerikus integrálás

  1. Implementálja a téglalap és a trapéz módszert!

    • Adjon rájuk szekvenciális és párhuzamos implementációt!

    • Hasonlítsa össze ezek futási idejét és becslési pontosságát (ismert értékű határozott integrálok esetében)!

    • Az eredményeket gyűjtse össze táblázatok és grafikonok formájában!