2. Előadás - Végrehajtási módok, modellek
Párhuzamos végrehajtási módok
A programok párhuzamos végrehajtását különböző formában, szinteken valósíthatjuk meg. Egy lehetséges felosztás az alábbi.
Hálózat szint
Több, egymással összekapcsolt számítógépet használunk.
Elsődlegesen az elosztott rendszerek témaköre foglalkozik ennek hatékony megvalósításával.
Hardver szint
A hardverek egy jelentős része önmagában is képes több műveletet párhuzamosan végrehajtani.
CPU szintű párhuzamosítás:
Instrukció szintű párhuzamosítás (Instruction Level Parallelism): out-of-order execution, speculative execution, branch prediction
Hyper-Threading: fizikai processzoronként 2 logikai processzor
Dedikált hardverként az egyik legszemléletesebb példa a videókártya. OpenCL, kernelek
https://en.wikipedia.org/wiki/Instruction-level_parallelism
https://en.wikipedia.org/wiki/Hyper-threading
Virtuális gépek
Egy számítógépen belül több operációs rendszer indítható el párhuzamosan.
Az erőforrások hatékonyan kihasználhatók különösebb szoftverfejlesztési feladat nélkül.
Folyamatok
Az operációs rendszer ütemezi a folyamatok működését. Amennyiben meg tudja oldani, úgy a párhuzamosan végrehajtható részeket párhuzamosan futtatja.
Több szekvenciális végrehajtású program időben párhuzamosan tud így futni.
Operációs rendszer szintjén felügyelhető a működés.
Egy számítási feladat szempontjából ezek kommunikációjával is megoldhatjuk a párhuzamosítást.
Inter Process Communication, MPI szabvány
Szálak
Egy programon belül mi magunk kijelölhetjük azokat a részeket, amelyek végrehajtása időben átfedésbe kerülhet.
A végrehajtás során nem garantált, hogy valóban párhuzamosan történik majd. (Az operációs rendszer dönti el.)
Könnyű súlyú szálak
A felhasználói térben (user space) kerülnek ütemezésre.
Szokták még nevezni zöld szálaknak, coroutine-oknak.
Mivel a szálak implementációja rendszerenként eltérő, ezért nincs pontos határvonal a szálak és a könnyűsúlyú szálak között.
A programozási nyelvekben egyedi megoldások vannak ezek használatára..
Memóriamodellek
\(\rhd\) Gondoljuk át a memória és a számítási elemek közötti 1:N, N:1, N:M kapcsolatokat!
Lokális memória
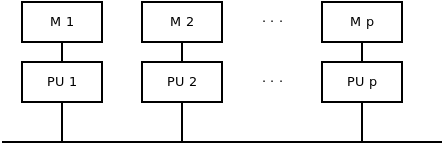
Moduláris memória
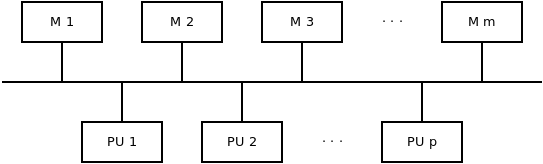
Osztott memória
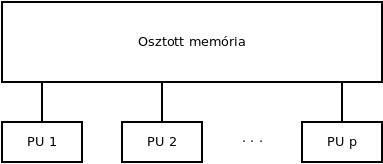
Cache
Cache update probléma
Kritikus szakasz
Kölcsönös kizárás
Hálózatok
A párhuzamos végrehajtási mód megvalósítási módjától függetlenül tudjuk vizsgálni a rendszerek topológiáját és a számítási egységek közötti kommunikációt.
Csomópontként jelöljük a számítási egységeket, esetlegesen a tárakat (memóriát, háttértárat).
Az élek a kommunikációs csatornákat jelölik.
A kommunikáció irányával külön is kellhet foglalkozni. Ilyen esetben irányított gráfokat használunk.
Nézzünk egy nagyon egyszerű példát egy ilyen topológiára!
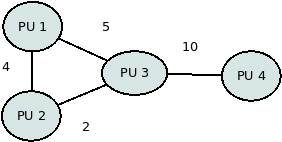
Elterjedt topológiák
Az alapvető probléma az, hogy egy üzenetet (csomagot) el kell juttatni az egyik állomástól a másikig.
A cél az, hogy ezt minél gyorsabban, hatékonyabban meg tudjuk tenni.
A hálózatra úgy tekinthetünk, hogy a csomag csak az élek mentén tud haladni.
Külön problémát jelent, hogy párhuzamosan több csomag is továbbításra kerül.
Elvileg tetszőleges gráf lehetne a topológia.
A következők elvi és praktikus okok miatt alakultak így.
Busz

Az egyik legegyszerűbb összeköttetési forma.
A csomópontokat célszerű indexelni, amelyeken így értelmezett egy rendezés.
Tekinthető a fa egy speciális esetének.
\(\rhd\) Mennyi az élek száma általános esetben?
\(\rhd\) Vizsgáljuk meg a \(p = 4\) esetre a csomópontok közötti távolságokat?
\(\rhd\) Adjuk meg a (0-nál nagyobb) távolságok eloszlását!
\(\rhd\) Mennyi a maximális és az átlagos távolság a csomópontok között?
Gyűrű

Célszerű itt is tudni, hogy merre felé van a címzett (de nem kötelező).
\(\rhd\) Mennyi az élek száma általános esetben?
\(\rhd\) Vizsgáljuk meg a \(p = 4\) esetre a csomópontok közötti távolságokat?
\(\rhd\) Adjuk meg a (0-nál nagyobb) távolságok eloszlását!
\(\rhd\) Mennyi a maximális és az átlagos távolság a csomópontok között?
Rács
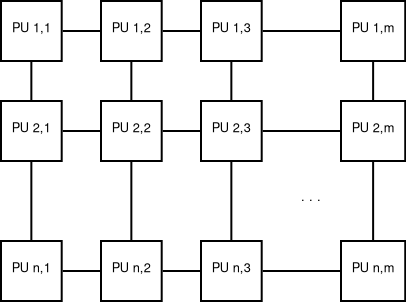
Tetszőleges dimenziós lehet, és nem csak négyzetes.
A címzést dimenziószám részből álló címekkel előnyös megoldani.
\(\rhd\) Mennyi az élek száma általános esetben?
\(\rhd\) Vizsgáljuk meg a távolságokat egy \(4 \times 4\) méretű rácsra!
\(\rhd\) Mennyi a maximális távolság egy \(n \times m\) méretű rácsban?
Tórusz
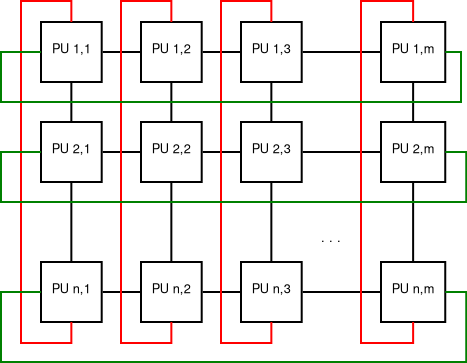
Szintén elképzelhető magasabb dimenziós és nem négyzetes változat is.
Az \(n\) és az \(m\) számú plusz él beiktatása jelentősen csökkenti a csomópontok közötti távolságokat.
\(\rhd\) Mennyi az élek száma általános esetben?
\(\rhd\) Hogyan változnak a távolságok a plusz összeköttetéssel egy \(4 \times 4\) méretű rácshoz képest?
Hiperkocka
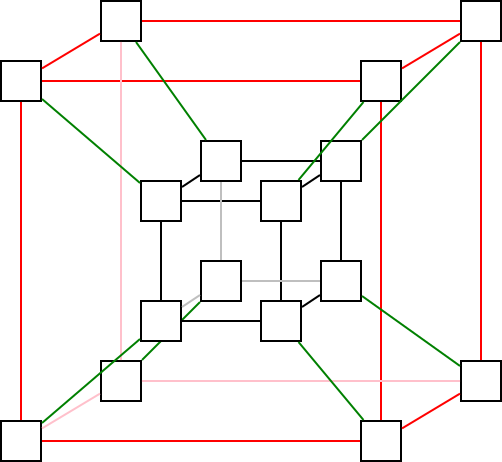
\(\rhd\) Hogyan tudjuk címezni a csomópontokat?
\(\rhd\) Adjuk meg, hogy a dimenziószám függvényében (például \(n\)-nel jelölve), hogyan változik a csomópontok és az élek száma! (Írjuk fel hozzá táblázatban 0-tól 8 dimenzióig a csúcsok (\(|V|\)) és élek (\(|E|\)) számát!)
\(\rhd\) Egy \(n\) dimenziós hiperkockában mennyi lesz a csomópontok közötti minimális és maximális távolság?
Fa
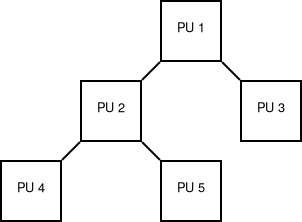
Egy összefüggő, körmentes gráf.
Szoktak még említeni csillag topológiát. Ezt tekinthetjük a fa speciális esetének.
\(\rhd\) Hogyan oldható meg a csomópontok címzése (és ezzel kapcsolatosan a routing)?
\(\rhd\) A példában szereplő fa esetében hogyan alakulnak a csomópontok közötti távolságok? Adjuk meg ezek eloszlását!
Fat-tree
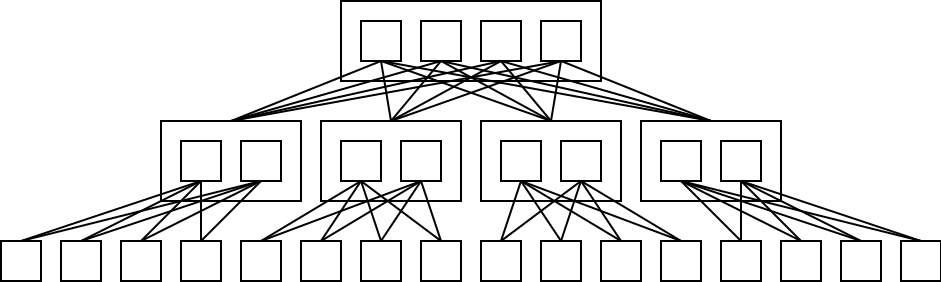
Arra a feltételezésre épül, hogy a magasabb szintek között nagyobb sávszélességre van szükség. (Az „Oszd meg és uralkodj!” elven működő algoritmusoknál igen gyakran ez a helyzet.)
Elvek és modellek
Leképzés (map)
Az egyik legegyszerűbb és leghatékonyabban párhuzamosítható algoritmus.
Tegyük fel, hogy adott egy \(x \in \mathbb{R}^n\) vektor! Ki szeretnénk számítani egy \(y \in \mathbb{R}^n\) vektort, melyre teljesül, hogy \(y_i = f(x_i), \forall i\), és \(f: \mathbb{R} \rightarrow \mathbb{R}\) egy tetszőleges valós függvény.
Hogyan változik a munka, költség, gyorsítás és hatékonyság \(p\) függvényében?
Osszd meg és uralkodj elv
Felosztás \(\rightarrow\) művelet \(\rightarrow\) egyesítés
Tipikusan rekurzív formában használatos
Figyelem
A felosztás megfelelő szintjének meghatározása külön érdekes problémakör! (Jellemzően nem szerencsés az elemek szintjéig lemenni.)
Pipeline párhuzamosítás
Tegyük fel, hogy vannak feldolgozandó elemeink, amelyeken adott sorrendben, mindig ugyanazokat a lépéseket kell végrehajtani.
Feltételezzük, hogy a lépések végrehajtási ideje közel egyenlő.
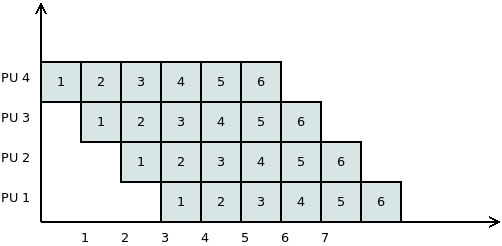
\(\rhd\) Mekkora gyorsítást tudunk így elérni?
\(\rhd\) Mennyire lesz ez a módszer hatékony? (Írjuk fel \(p\) és \(n\) függvényében!)
Termelő-fogyasztó probléma
Task pool
Gyors válaszidő, terhelés kiegyenlítés érdekében használják például.
Általában sort használnak hozzá.
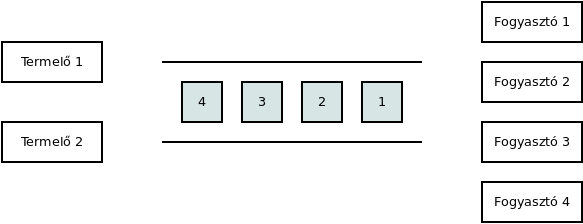
\(\rhd\) Milyen előnyei vannak a módszernek?
\(\rhd\) Milyen eseteket nem tud jól kezelni?
Lost Update probléma
Példa
Feltételezzük, hogy A és B egy változó értékét szeretné módosítani. A következő műveletek kerülnek végrehajtásra.
A kiolvassa a változó értékét.
B kiolvassa a változó értékét.
A növeli a változó értékét.
B növeli a változó értékét.
Zárolási mechanizmusok
Garantálnunk kell tudni, hogy adott erőforrásokhoz egyidejűleg csak egy valaki férhet hozzá.
Lakat (Lock)
Egy jelzőbittel (flag-gel) megoldható.
Jelezni kell, hogy mikor foglaljuk le, és mikor szabadítjuk fel az erőforrást.
Szemafor
Egy számláló, amely nyilvántartja a lefoglalások és felszabadítások számát.
Kérdések
Mennyi a 0-nál nagyobb távolságok eloszlása egy 7 csomópontból álló buszon?
Mennyi az átlagos távolság egy 8 csomópontból álló gyűrűben?
Egy \(6 \times 6 \times 6\) rács esetében mennyi élünk lesz? Mennyi lesz a csomópontok közötti maximális távolság?
Mennyi csomópont és él lesz egy 5 dimenziós hiperkockában? Mennyi ez esetben a maximális távolság?
Feladatok
Szekvencia diagram
Keressen példákat szekvencia diagramokra az Interneten! Vizsgálja meg, hogy miben hasonlítanak és különböznek a jelölések!
Tegyük fel, hogy egy tanár 2 hallgatóval írat dolgozatot. A tanár sorban kiosztja a feladatsort. A hallgatók megoldják a feladatokat, majd beadják ahogy elkészültek. A tanár kiértékeli (egyszerre csak egyet), visszaadja a hallgatóknak átnézésre, majd visszakéri a dolgozatokat. Rajzoljon fel egy lehetséges szekvencia diagramot a dolgozat írásához!
Feladatmegosztás optimalizálása
Tegyük fel, hogy adott 2 gép, melyek hálózaton keresztül tudnak kommunikálni.
A feladatokat egységnyieknek tekintjük.
Összesen 3000 feladat van.
Az első gép 1 feladatot 10 másodperc alatt old meg, a második pedig 5 másodperc alatt.
A bemenet az első gépen áll rendelkezésre.
A második gépre való küldés 2 másodpercet igényel feladatonként.
A küldés és fogadás ideje alatt a gépek nem tudnak lényegi számítást végezni.
Az eredményeknek az első gépre kell kerülniük.
Hogyan ossza meg a két gép a feladatokat, hogy a lehető legkevesebb ideig tartson összességében?
Vezessünk be jelöléseket!
Próbáljuk meg általánosan is megoldani a problémát!
Ábrázoljuk grafikonon a párhuzamos végrehajtás idejét!
Mérések algoritmusok bonyolultságára vonatkozóan
Készítsen el egy programot, amellyel egy tömbben lévő számértékeket lehet beolvasni.
Írjon egy függvényt az elemek összegének kiszámításához!
Valósítsa meg a minimum és a maximum értékének a meghatározását külön függvényekben!
Próbálja meg rekurzív függvényekkel is megoldani az előbbi számítási feladatokat!
Mérje le, gyűjtse össze táblázatba és ábrázolja grafikonon az iteratív és a rekurzív változatok számítási idejét az elemszám függvényében!
Adjon felső becslést a futási időre vonatkozóan! (\(T(n) = \mathcal{O}(?)\))
Generáljon egy tömböt úgy, hogy az elemek egész értékűek, és mindegyik különbözik!
Vizsgálja meg a tömb generálásának számítási idejét az elemszám függvényében!
0.5 valószínűséggel duplikáljon benne néhány elemet!
Készítsen olyan függvényt, amely ellenőrzi, hogy a tömb minden eleme egyedi-e!
Vizsgálja meg a függvény bonyolultságát!
Generáljon egy tömböt, amelyben az elemek lebegőpontos értékek, és szigorúan monoton növekvő sorozatot alkotnak!
Készítsen függvényt a tulajdonság ellenörzéséhez!
Definiáljon egy függvényt, amely bináris kereséssel keres egy elemet a tömbben!
Készítse el az iteratív és a rekurzív változatát!
Véletlenszerűen kiválasztott és/vagy generált értékek keresése alapján mérje le a számítási idők eloszlását (adott elemszám mellett)!
Hasonlítsa össze az iteratív és a rekurzív változat futási idejét az elemszám függvényében!
Ábrázolja az egyes elemszámokhoz tartozó futási idők maximumát!
Generáljon egy szöveges fájlt az angol ábécé kis és nagy betűiből, számjegyekből, szóközökből és sortörésekből véletlenszerűen!
A generáláshoz paraméterként használja a generálandó karakterek számát!
Készítsen egy függvényt, amelyik meghatározza, hogy mennyi sort tartalmaz a szöveges fájl!
Próbáljon rekurzív megoldást is adni a problémára!
Hasonlítsa össze az iteratív és a rekurzív változat futási idejét!
Határozza meg az üres sorok számát!
Prefix számítás vizsgálata
Tekintsük a prefix számítás esetében egységnyi idejűnek a \(\oplus\) művelet elvégzését!
Készítsen egy programot, amely a CREW_PREFIX algoritmus végrehajtása során elvégzett hívásokat GraphViz segítségével egy hívási fában ábrázolja!
A program a kimenetet egy szöveges fájl formájában adja meg!
A megjelenítéshez használhat online gráf megjelenítőt, például: https://dreampuf.github.io/GraphvizOnline/
A csomópontokban tüntesse fel, hogy a hívás milyen intervallumra vonatkozott!
Próbálja megoldani, hogy a program tetszőleges \(n\) méretű bemenetre működjön!
Az EREW_PREFIX algoritmus vizsgálatához készítsen egy programot, amellyel vizsgálható a párhuzamosan elvégzett számítások során a munka, költség, gyorsítás és a hatékonyság mértéke!
Egy szövegfájlba mentse le, hogy a számítások során a \(t\) időpillanatban mennyi számítási egység végzett éppen hasznos munkát! (Itt a sorok mutassák az időt, az oszlopok pedig, hogy melyik számítási egységről van szó! Jelölje
.karakter, hogy ha nem történt hasznos számítás,#pedig hogy ha igen!)Határozza meg az említett \(W\), \(C\), \(S\) és \(E\) értékeket \(n = 100\) bemenetméretig!
Gyűjtse össze az adatokat egy táblázatba!
Ábrázolja grafikonon a bemenet függvényében a gyorsítás és a hatékonyság mértékét!
Vizsgálja meg az OPTIMAL_PREFIX algoritmus működését!
Írjon fel egy saját példát \(n = 16\) bemenet esetére! Rajzolja fel az ehhez tartozó Gantt diagramot!
Ábrázolja grafikonon, hogy \(n\) méretű bemenet esetén mennyi processzorra van szükség a számításhoz!
Karakter tömb segítségével ábrázolja (például fájlba kimentve), hogy a \(t.\) időegységben végzett-e hasznos számítást a \(p.\) processzor!
Határozza meg az említett \(W\), \(C\), \(S\) és \(E\) értékeket \(n = 100\) bemenetméretig!
Hálózati topológiák
Négyzetes rács topológia esetén végezze el a következő számításokat!
Számítsa ki \(n = 50\)-ig, hogy egy \(n \times n\) méretű rácsban mennyi csomópont és él van!
Határozza meg ezek arányát \(n\) függvényében, és ábrázolja a kapott eredményt grafikonon!
Egy \(12 \times 12\)-es méretű rács esetében határozza meg a pontok közötti távolságok eloszlását!
Ábrázolja a kapott eredményt hisztogramon!
Vizsgálja meg, hogy \(n = 24\)-ig térbeli rács esetében hogyan változik a csomópontok és élek száma!
Hasonlítsa össze, hogy \(n\) függvényében hogyan alakul az élek száma síkbeli és térbeli rácsok esetében!
Számítsa ki a csomópontok közötti távolságok eloszlását egy \(5 \times 5 \times 5\) méretű térrácsban!
Végezze el az előbbi számításokat tórusz topológia esetében!
Végezzen számításokat hiperkocka topológia esetében!
Számítsa ki, hogy 30 dimenzióig hogyan változik a csomópontok és az élek száma!
Határozza meg 8 dimenzióban a csomópontok közötti távolságok eloszlását!
Ábrázolja a kapott eredményt hisztogramon!
Számítsa ki 20 dimenzióig az átlagos távolságokat!
Hasonlítsa össze ezeket a csomópontok száma alapján a síkbeli és térbeli rács topológiákkal!