7. Strukturált programozás¶
Strukturáltság
Általában fa struktúrát érthetünk alatta.
A problématerünket egymásba ágyazott diszjunkt részhalmazokra bontjuk.
Az ágakat gyakran rendezettnek tekintjük.
Lokalitás, esetek szétválasztása
C,
struct
Két program ekvivalenciája
Két programot ekvivalensnek nevezünk, hogy ha az összes lehetséges bemenet esetében azonos bemenetekre azonos kimeneteket eredményeznek.
A program állapotát, mint egy pontot tekintve az állapottérben azt is mondhatjuk, hogy azonos kezdőpontból azonos végpontba jutnak el.
Programgráf / Vezérlési gráf
Olyan összefüggő, irányított gráf, amely
vonalakból (folyamatvonalakból),
szekvenciákból (függvényekből),
elágazásokból (predikátum egy befutó, két kifutó éllel),
gyűjtőpontokból (két befutó, egy kifutó él)
épül fel.
Teljes élhalmazos jelölés
Minden csomóponthoz rendelünk valamilyen betűjelölést.
A gráfot, mint élek halmazát adjuk meg.
Elágazás esetén az igaz és a hamis esetet az élhez külön jelölni kell.
Tömör élhalmazos jelölés
Az éleket az áttekinthetőség kedvéért csak nyilakkal adjuk meg.
A gyűjtőpontokat külön nem jelöljük.
Valódi program
Egy programot valódi programnak nevezünk, hogy ha
programgráfja véges számú bemenő és kimenő éllel rendelkezik,
programgráfjának csomópontjai predikátumok, függvények és gyűjtőpontok,
a programgráfjának minden pontján keresztül vezet útvonal, amely a belépési ponttól a kilépési pontig tart.
\(\rhd\) Adjunk példát nem valódi programokra, melyek a felsorolt feltételekből csak egyet-egyet nem teljesítenek!
Strukturált alapelemek¶
Elemek jelölési módjai
Formula
Programgráf
Struktogram (Nassi-Schneidermann ábra)
Szekvencia¶
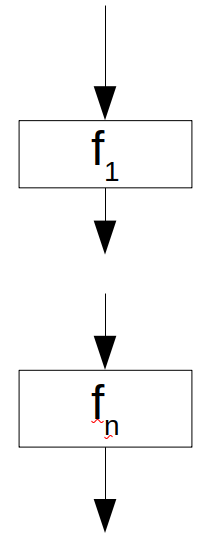
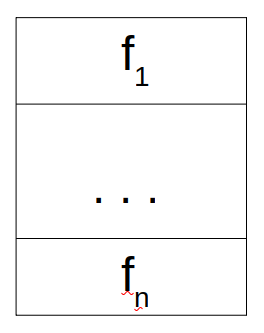
Elágazás¶
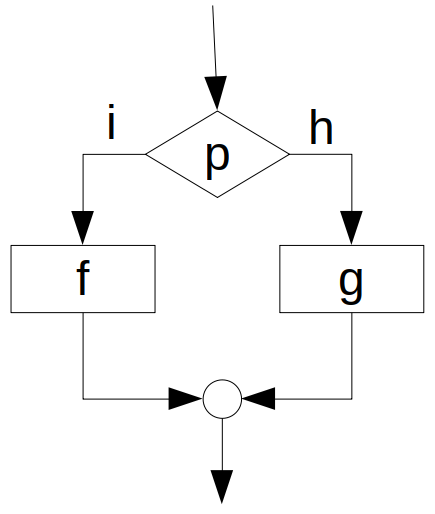
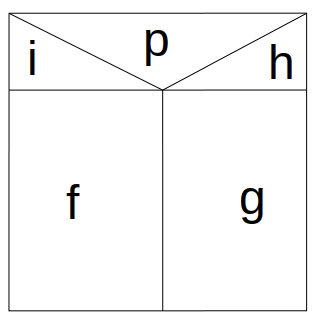
Ciklus¶
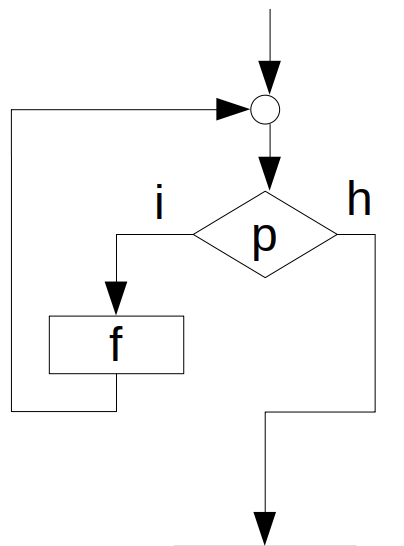
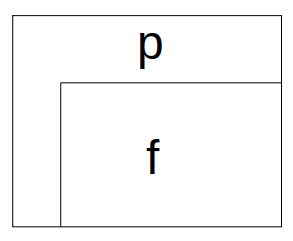
Kvázi strukturált alapelem¶
Iteráció¶
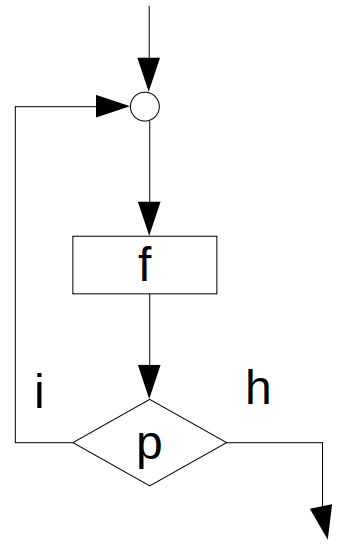
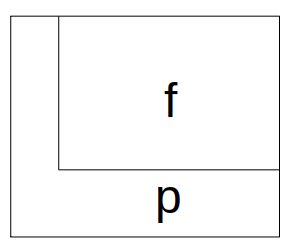
Egyszerűen belátható, hogy
Minden strukturált alapelemnek pontosan egy belépési és egy kilépési pontja van.
\(\rhd\) Milyen előnyei és hátrányai vannak az egyes jelölési módoknak?
Strukturált programok¶
Vezérlőgráf lebontása
Vezérlőgráf lebontásának nevezzük azt az eljárást, amelyben minden lépésben egy strukturált alapelemet egy függvénycsomóponttal helyettesítünk. Ezt addig folytatjuk, ameddig lehetséges.
Az egyetlen csomópontból álló gráfot egyetlen irányított élre cserélünk (melyet üres programnak nevezünk).
Strukturált program
Strukturált programnak nevezzük az olyan programot, amely programgráfja lebontható az önmagában álló irányított élre.
\(\rhd\) Lássuk be, hogy a definíció fordított lépések sorozatával is megadható lett volna!
Strukturált program formulája
Egy program csak akkor strukturált, hogy ha a formulája felírható a szekvencia, elágazás és a ciklus formulájából.
Böhm-Jacopini tétel
Minden valódi program megadható ekvivalens, strukturált program formájában.
A tétel csak azt mondja ki, hogy megadható, de közvetlenül az átírás formáját nem részletezi.
Az átírás nem egyértelmű. (Általában több ekvivalens strukturált program is megadható.)
Segédváltozó használata
Bizonyos esetekben a strukturált program felírása csak segédváltozó bevezetésével oldható meg. Ehhez egy flag nevű segédváltozót fogunk használni, amelyhez a következő műveletek tartoznak hozzá:
flag \(\leftarrow\) igaz: a segédváltozó értékét beállítja igaz értékre,
flag \(\leftarrow\) hamis: a segédváltozó értékét beállítja hamis értékre,
flag = igaz: egy predikátum, amely a segédváltozó értéke alapján dönt,
FREE(flag): felszabadítja a lefoglalt segédváltozót.
\(\rhd\) Adjunk példát nem strukturált programra, amelyben predikátum predikátumot követ!
\(\rhd\) Írjuk fel az ekvivalens strukturált programot (az előforduló jelölési módokkal)!
\(\rhd\) Lássuk be, hogy a kapott program valóban strukturált!
Programok bonyolultsága¶
Programgráf ciklikus bonyolultsága
A \(P\) programgráf ciklikus bonyolultságának nevezzük az \(m(P) = e - c\) értéket, ahol \(e\) az élek száma, \(c\) pedig a csúcsok száma a programgráfban.
Programgráf ciklikus bonyolultságának a tétele
Egy programgráf ciklikus bonyolultsága az \(m(P) = p + 1\) formában is számolható, ahol \(p\) a programgráfban lévő predikátumok számát jelöli.
Bizonyítás
Vezessük be a következő jelöléseket!
\(p\): predikátumok száma
\(f\): függvénycsomópontok száma
\(g\): gyüjtőpontok száma
\(e\): élek száma
\(c\): csúcsok száma
Könnyen látható, hogy \(c = p + f + g\).
Határozzuk meg az élek számát a bemenő és a kimenő éleket tekintve:
Tegyük ezt a kettőt egyenlővé egymással:
amiből azt kapjuk, hogy
A csúcsok és élek számát tehát a következő formában is felírhatjuk:
Visszahelyettesítve a ciklikus bonyolultság képletébe, egyszerűen adódik a tétel állítása:
Nem strukturált program ciklikus bonyolultságának tétele
Hogy ha \(P\) egy nem strukturált program, akkor annak programgráfjának ciklikus bonyolultsága legalább 3, vagyis \(m(P) \geq 3\).
Programgráf lényeges bonyolultsága
Egy programgráf lényeges bonyolultságát az \(M(P) = m(P) - k\) formában definiáljuk, ahol \(k\) a programgráfban elvégezhető lebontási lépések maximális száma, amelyben predikátumot vettünk ki a gráfból.
Strukturált program lényeges bonyolultságának tétele
A strukturált programok lényeges bonyolultsága mindig 1, tehát \(M(P) = 1\), hogy ha \(P\) strukturált.
Bizonyítás
A lényeges bonyolultság az \(M(P) = m(P) - k\) formában számolható. Strukturált program esetében \(k = p\), így
Kérdések¶
Van-e olyan program, amelyik strukturált, de nem valódi? Ha igen, akkor adjon rá példát, ha nincs, akkor miért nincs?
Garantálja-e a struktogram felrajzolása, hogy a program valódi?
Garantálja-e a struktogram felrajzolása, hogy a program strukturált?
Feladatok¶
A következő, tömör élhalmazos formában megadott programokhoz készítsünk
programgráfot,
írjuk fel az eredeti és az ekvivalens struktúrált program pszeudó kódját,
rajzoljuk fel a struktogramot,
írjuk fel a formuláját,
számítsuk ki a ciklikus és a lényeges bonyolultságot!