3. Logikai adattípus és műveletei

Logikai értékek

\[L = \{0, 1\}\]

Rengeteg elterjedt alternatív jelölés van:

  • hamis, igaz

  • false, true

  • h, i

  • F, T

A logikai absztrakt adattípus:

\[T = (L, M)\]

Logikai műveletek

  • Az operandusok száma szerint tudjuk csoportosítani őket.

  • Az \(L\) halmaz végessége miatt az összes műveletet fel tudjuk sorolni.

Egyváltozós műveletek

\(x\)

0

\(x\)

\(\overline{x}\)

1

0

0

0

1

1

1

0

1

0

1

  • Az első oszlop tartalmazza a behelyettesítendő értékeket.

  • A további oszlopokban az unáris műveletek szerepelnek.

Műveletek neve:

  • 0: konstans hamis

  • \(x\): identikus függvény

  • \(\overline{x}\): negáció, tagadás, NOT

  • 1: konstans igaz

A negáció műveletét szokás még így is jelölni: \(\neg x\)

Kétváltozós műveletek

\(x\)

\(y\)

\(x \wedge y\)

\(x \vee y\)

\(x \oplus y\)

\(x \leftrightarrow y\)

\(x \rightarrow y\)

\(x \downarrow y\)

\(x \mid y\)

0

0

0

0

0

1

1

1

1

0

1

0

1

1

0

1

0

1

1

0

0

1

1

0

0

0

1

1

1

1

1

0

1

1

0

0

  • Az első 2 oszlop a bemeneteket tartalmazza.

  • A további oszlopokban a gyakrabban használt függvények szerepelnek.

Figyelem

A felsoroltakon kívül is vannak még kétváltozós műveletek!

  • \(x \wedge y\): „és”, AND, konjunkció

  • \(x \vee y\): „vagy”, OR, diszjunkció

  • \(x \oplus y\): „kizáró vagy”, antivalencia

  • \(x \leftrightarrow y\): ekvivalencia

  • \(x \rightarrow y\): implikáció

  • \(x \downarrow y\): Pierce nyíl

  • \(x \mid y\): Scheffer vonás

\(n\)-változós műveletek

  • Az előzőekhez hasonlóan fel tudnánk sorolni a 3 vagy annál több operandusú műveleteket is.

  • A gyakorlatban ezekre ritkábban van szükség egy művelet formájában.

Minden \(n\)-változós műveletet fel tudunk írni egy- és kétváltozós műveletek segítségével. Emiatt a logikai adattípust definiálhatjuk például a következő formában:

\[T = (\{0, 1\}, \{\neg, \wedge, \vee\})\]

Műveletek száma

Az \(n\)-változós logikai műveletek száma \(2^{2^n}\).

Műveleti azonosságok

Kettős tagadás

\[\overline{\overline{x}} = x\]

Kommutativitás

\[x \wedge y = y \wedge x, \quad x \vee y = y \vee x\]

Asszociativitás

\[(x \wedge y) \wedge z = x \wedge (y \wedge z), \quad (x \vee y) \vee z = x \vee (y \vee z)\]

Disztributivitás

\[ x \wedge (y \vee z) = (x \wedge y) \vee (x \wedge z), \quad x \vee (y \wedge z) = (x \vee y) \wedge (x \vee z)\]

De Morgan azonosság

\[\overline{x \wedge y} = \overline{x} \vee \overline{y}, \quad \overline{x \vee y} = \overline{x} \wedge \overline{y}\]

További összefüggések

\[\begin{split}x \wedge 0 = 0, \quad x \vee 0 = x \\ x \wedge x = x, \quad x \vee x = x \\ x \wedge \overline{x} = 0, \quad x \vee \overline{x} = 1 \\ x \wedge 1 = x, \quad x \vee 1 = 1 \\\end{split}\]

Antivalencia

\[x \oplus y = (\overline{x} \wedge y) \vee (x \wedge \overline{y}) = (x \vee y) \wedge (\overline{x} \vee \overline{y})\]

Ekvivalencia

\[ x \leftrightarrow y = (x \wedge y) \vee (\overline{x} \wedge \overline{y}) = (\overline{x} \vee y) \wedge (x \vee \overline{y})\]

Implikáció

\[x \rightarrow y = \overline{x} \vee y\]

Normálformák

  • Ugyanazon logikai függvény különböző formában is felírható (ahogy például az azonosságoknál is láthattuk.)

  • A normálforma a lehetséges felírások egy leszűkítését jelenti.

Diszjunktív normálforma

Elemi konjunkció

Változók vagy negáltjaiknak a konjunkciója, melyben a változók legfeljebb egyszer fordulhatnak elő.

Diszjunktív normálforma

Elemi konjunkciók diszjunkciója.

DNF: Diszjunktív Normál Forma

Példa

Határozzuk meg az \(f(x, y, z) = x \oplus (z \rightarrow y)\) diszjunktív normál formáját!

\(x\)

\(y\)

\(z\)

\(z \rightarrow y\)

\(x \oplus (z \rightarrow y)\)

elemi konjunkciók

0

0

0

1

1

\(\overline{x} \wedge \overline{y} \wedge \overline{z}\)

0

0

1

0

0

0

1

0

1

1

\(\overline{x} \wedge y \wedge \overline{z}\)

0

1

1

1

1

\(\overline{x} \wedge y \wedge z\)

1

0

0

1

0

1

0

1

0

1

\(x \wedge \overline{y} \wedge z\)

1

1

0

1

0

1

1

1

1

0

DNF:

\[f(x, y, z) = (\overline{x} \wedge \overline{y} \wedge \overline{z}) \vee (\overline{x} \wedge y \wedge \overline{z}) \vee (\overline{x} \wedge y \wedge z) \vee (x \wedge \overline{y} \wedge z)\]

Konjunktív normálforma

Elemi diszjunkció

Változók vagy negáltjaiknak a diszjunkciója, melyben a változók legfeljebb egyszer fordulhatnak elő.

Konjunktív normálforma

Elemi diszjunkciók konjunkciója.

KNF: Konjunktív Normál Forma

Példa

Határozzuk meg az \(f(x, y, z) = (z \leftrightarrow z) \vee y\) konjunktív normál formáját!

\(x\)

\(y\)

\(z\)

\(z \leftrightarrow x\)

\((z \leftrightarrow z) \vee y\)

elemi diszjunkciók

0

0

0

1

1

0

0

1

0

0

\(x \vee y \vee \overline{z}\)

0

1

0

1

1

0

1

1

0

1

1

0

0

0

0

\(\overline{x} \vee y \vee z\)

1

0

1

1

1

1

1

0

0

1

1

1

1

1

1

KNF:

\[f(x, y, z) = (x \vee y \vee \overline{z}) \wedge (\overline{x} \vee y \vee z)\]

Logikai kapuáramkörök

  • A logikai műveleteket reprezentálhatjuk grafikusan kapukkal.

  • A kapuknak a bal oldalán van a bemenetük, jobb oldalán pedig a kimenetük.

  • A kaput téglalapként ábrázoljuk, melybe beleírjuk az általa végrehajtott műveletet.

  • A nem kommutatív műveletek (például implikáció) esetében a bemeneteket fenntről-lefelé haladva tekintjük.

  • A nem használt bemeneteket és kimeneteket jelöljük úgy, hogy egy üres karikához kötjük.

Például

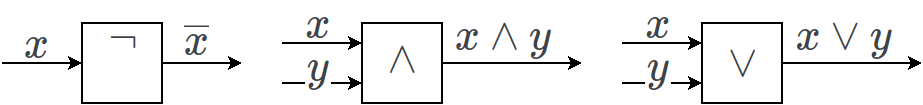
../_images/gates.png

Összeadó logikai áramkörök

Bináris formában adott egészek összeadására használható logikai kapuáramkör.

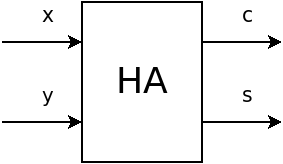
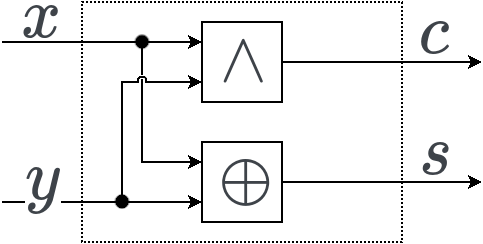
Félösszeadó

HA: Half Adder

Művelettábla

\(x\)

\(y\)

\(c\)

\(s\)

0

0

0

0

0

1

0

1

1

0

0

1

1

1

1

0

  • \(x\), \(y\): Az összeadandó értékek

  • \(c\): átviteli bit (carry)

  • \(s\): összeg (sum)

\[c = x \wedge y, \quad s = x \oplus y\]

Logikai kapu

../_images/half_adder.png

Belső felépítése

../_images/half_adder_inner.png

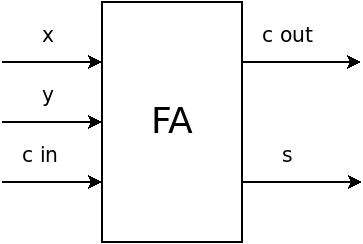
Egész összeadó

FA: Full Adder

Művelettábla

\(x\)

\(y\)

\(c_{\text{in}}\)

\(c_{\text{out}}\)

\(s\)

0

0

0

0

0

0

1

0

0

1

1

0

0

0

1

1

1

0

1

0

0

0

1

0

1

0

1

1

1

0

1

0

1

1

0

1

1

1

1

1

  • \(x\), \(y\): Az összeadandó értékek

  • \(c_{\text{in}}\): bemeneti átviteli bit

  • \(c_{\text{out}}\): kimeneti átviteli bit

  • \(s\): összeg (sum)

Logikai kapu

../_images/full_adder.png

Belső felépítése

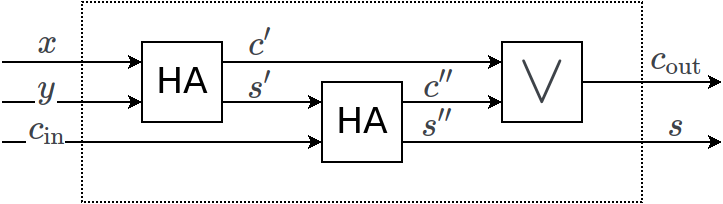
../_images/full_adder_inner.png

Több bites összeadó

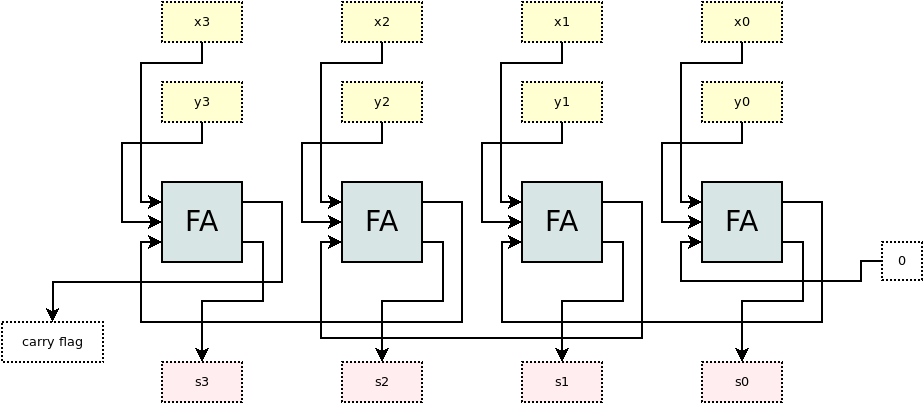
../_images/adder_4_bit.png

Bitműveletek

A programozási nyelvek különböző mértékben támogatják a bitműveleteket.

x & y;    // AND
x | y;    // OR
x ^ y;    // XOR
~x;       // Bitwise NOT
x << n;   // Shift left by n bits
x >> n;   // Shift right by n bits

Többértékű logikák

https://en.wikipedia.org/wiki/Many-valued_logic

  • Az igaz és hamis mellett további értékek is megjelenhetnek.

\(x\)

\(\overline{x}\)

0

1

?

?

1

0

Kleene

\(\wedge\)

0

?

1

0

0

0

0

?

0

?

?

1

0

?

1

\(\vee\)

0

?

1

0

0

?

1

?

?

?

1

1

1

1

1

Bochvar

\(\wedge\)

0

?

1

0

0

?

0

?

?

?

?

1

0

?

1

\(\vee\)

0

?

1

0

0

?

1

?

?

?

?

1

1

?

1

Folytonos logikák

  • Fuzzy logika

  • Intuícionista logikák

Kérdések

  • A lehetséges 16 bináris művelet közül melyek a kommutatívak és a nem kommutatívak?

  • Mennyi 5 változós logikai művelet van?

Feladatok

Normál formák

  • Írjuk fel a 3 bemenetes többségi szavazás diszjunktív normál formáját, és rajzoljuk fel a kapuáramkört!

  • Tervezzünk 4 bemenetes paritás ellenörző automatát!

  • Fejezzük ki az antivalencia, implikáció és az ekvivalencia műveleteket az \(\wedge, \vee\) és negáció műveletekkel!

  • Tervezzünk 5 bemenetes automatát, amely a maximumot adja vissza! Írjuk fel a diszjunktív és a konjunktív normál formáját!

  • Tervezzünk kapuáramkört az \(\wedge, \vee, \neg\) műveletekkel az \(u = f(x, y, z) = (x \oplus y) \rightarrow z\) logikai függvényhez, és írjuk fel a diszjunktív normál formáját!

  • Írjuk fel az implikáció műveletének diszjunktív és konjunktív normál formáját!

  • Egy függvény DNF-je \((x \wedge \overline{y} \wedge z) \vee (\overline{x} \wedge \overline{y} \wedge z)\). Írja fel a függvény konjunktív normál formáját!

  • Írjuk fel a Scheffer vonás és a Pierce nyíl DNF-jét és KNF-jét!

  • A \(0\) és \(1\) értékeket, mint egész értékeket tekintve adjuk meg a \(<, >, \leq, \geq, =, \neq\) logikai operátorok művelettábláját!

  • Írjuk fel a minimum és a maximum függvények művelettábláját 3 változó esetén!

Függvények kiértékelése

Művelettáblájuk alapján ismerjük az \(f\) és a \(g\) három változós logikai függvényeket.

\(x\)

\(y\)

\(z\)

\(f(x, y, z)\)

\(g(x, y, z)\)

0

0

0

1

0

0

0

1

0

0

0

1

0

0

1

0

1

1

1

1

1

0

0

1

1

1

0

1

1

0

1

1

0

0

0

1

1

1

0

1

Definiáljunk egy \(h\) függvényt a következőképpen:

\[h(x, y, z) = g(x \oplus f(y \rightarrow z, x, z))\]

Határozzuk meg a \(h(1, 0, 0)\), \(h(0, 1, 0)\) és a \(ḣ(0, 1, 1)\) értékeket!

Azonosságok, levezetések

  • Írjuk fel a bináris műveleteket Scheffer vonás felhasználásával!

  • Lássuk be, hogy a Scheffer vonás nem asszociatív!

  • Lássuk be, hogy a Scheffer vonás nem disztributív az implikáció műveletére nézve!

  • Lássuk be, hogy az ekvivalencia művelete asszociatív!

  • Lássuk be a következőket!

\[\begin{split}&x \wedge (y \oplus z) = (x \wedge y) \oplus (x \wedge z) \\ &(p \wedge q \wedge r) \rightarrow s = p \rightarrow (q \rightarrow (r \rightarrow s)) \\ &(p \wedge (p \rightarrow q)) \rightarrow q = 1 \\ &(a | b) \oplus (a \downarrow b) = a \oplus b \\\end{split}\]

  • Vizsgáljuk meg az alábbi azonosságokat!

\[\begin{split}&a \rightarrow ((b|a) \wedge \overline{b}) = a \\ &\overline{a \wedge \overline{b \wedge \overline{c \wedge d}}} = \overline{\overline{\overline{a \wedge b} \wedge c} \wedge d} \\ &\overline{(x \oplus y) \rightarrow z} = (x \wedge \overline{y} \wedge \overline{z}) \vee (\overline{x} \wedge y \wedge \overline{z}) \\ &(a|b) \downarrow (c|d) = (d|a) \downarrow (c|b) \\\end{split}\]

  • Tekintsük a \(<\) és a \(\leq\) relációs jeleket, mint bináris logikai operátorokat. Lássuk be, hogy az alábbi összefüggés a negációt valósítja meg!

\[x < (x \leq x)\]

  • Lássuk be, hogy a \(\downarrow\) (Pierce nyíl) segítségével az összes logikai függvény felírható!

Logikai kapuáramkörök

  • Készítsünk egy logikai kapuáramkört, amelyik 3 bit bemenetre visszaadja bináris formában, hogy mennyi 1-es érték volt benne!

  • Készítsünk egy 8 bemenetes, 1 kimenetes logikai kapuáramkört, amely egy előjel nélküli egész értékről meg tudja állapítani, hogy 15-nél nagyobb-e!

  • Készítsünk egy 8 bemenetes, 1 kimenetes logikai kapuáramkört, amely jelzi, hogy a bemenetén kapott érték az egy pozitív páratlan szám-e!