5. A grafikus megjelenítési folyamat

A teljes megjelenítési folyamatot, mint egy transzformációs láncot képzelhetjük el.

Mivel egy cső, futószalag szerű feldolgozásról van szó, ezért ezt szokták nézeti csővezeték nek, vagy angolul rendering pipeline -nak hívni.

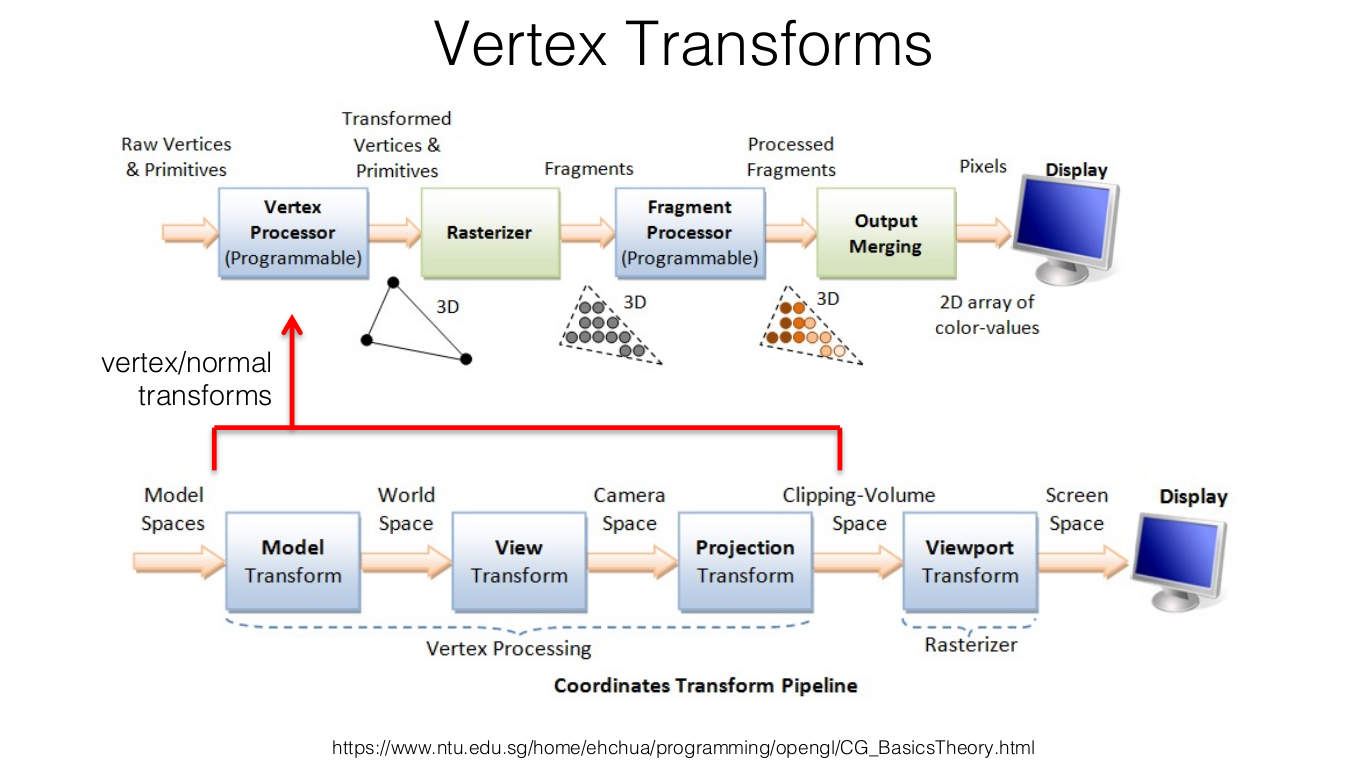
../../_images/pipeline.png

A megjelenítési folyamathoz tartozó fő transzformációk tehát:

  • Modell transzformáció,

  • Nézeti transzformáció,

  • Vetítési transzformáció,

  • Képtér transzformáció.

A modellek és a kamera transzformációját a korábbi témákból már ismerjük. Aktuálisan azt vizsgáljuk, hogy milyen további módszerek szükségesek ahhoz, hogy valószerűbbé, és hatékonyabbá tehessük a megjelenítést.

Láthatóság

A vetítési transzformációk önmagukban nem garantálják, hogy csak az látszódjon a képen, aminek a kamerából ténylegesen kellene. Az objektumok kirajzolásának sorrendjétől függhet az, hogy mi látszik majd a képen.

Takarási problémaként hivatkozunk arra a feladatra, amely során megállapítjuk, hogy a színtér mely részeinek kell látszódnia, és melyek lesznek takarásban az eredményként kapott képen.

Mivel a festésnél is hasonló problémáról van szó, ezért a közvetlen sorbarendezést használó algoritmust szokták nevezni painter’s algorithm-nek is:

../../_images/painters_algorithm.png

Az algoritmusnak nem minden esetben lehet egyáltalán megoldása, hogy ha egy objektum kirajzolását egy elemi lépésnek tekintjük.

\(\rhd\) Adjunk példát olyan esetre, amelyet sorbarendezéssel nem lehet megoldani!

A következőkben a láthatósági probléma lehetséges megközelítéseit vizsgáljuk.

Objektumok sorba rendezése

Egyszerűbb (speciális) esetekben megtehetjük azt, hogy előre meghatározzuk az objektumok megjelenítési sorrendjét, és a szerint rajzoltatjuk ki őket.

  • Feltételezzük, hogy egy-egy objektumot önmagában megfelelően meg tudunk jeleníteni. (Konvexek, és a hátsó lapjaik nem látszódnak.)

  • A sorrend meghatározása függ az összes objektum és a kamera pozíciójától is.

  • Általános esetben nem oldja meg a problémát.

\(\rhd\) Vizsgáljuk meg egy-egy konkrét esetre, hogy hogyan tudnánk megoldani a sorbarendezést!

Háromszögek sorba rendezése

Egy fokkal általánosabb megoldást kapunk, hogy ha az objektumok kirajzolásához használt háromszögeket rendezzük sorba.

  • Lényegesen nagyobb a számításigénye, mint az objektum szintű rendezésnek.

  • Az egymást metsző háromszögek problémájával nem tud mit kezdeni.

Z-buffer

A láthatóság vizsgálatát képpontok szintjén szeretnénk elvégezni. Ehhez definiálunk egy buffert, amely a megjelenített térbeli pont kamerától vett távolságát tartalmazza.

Amikor egy képpontot meg szeretnénk jeleníteni, akkor először

  • kiszámítjuk, hogy az milyen távolságra van a kamerától,

  • hogy ha ez a távolság kisebb, mint a Z-buffer adott helyen vett értéke, akkor megjelenítjük, és felülírjuk a Z-buffer értékét,

  • hogy ha nem, akkor felhagyunk a képpont megjelenítésével.

A módszer előnye, hogy

  • általánosan megoldja a takarási problémát, és

  • egyszerűen implementálható.

Hátránya, hogy

  • külön buffer szükséges a mélységértékek tárolásához. (Manapság ez már nem lényegi probléma.)

  • Az átlátszóságot, féligátlátszóságot nem tudja kezelni. (Egy közeli átlátszó elem „kitakarja” a mögötte lévő objektumokat.)

\(\rhd\) Vizsgáljuk meg két egymás mögötti négyzetre, hogy hogy működik az alkalmazás, hogy ha be-, és ha kikapcsoljuk a Z buffert!

glBegin(GL_QUADS);

glColor3f(1, 0, 0);
glVertex3f(0, 0, 0);
glVertex3f(0, 0, 1);
glVertex3f(1, 0, 1);
glVertex3f(1, 0, 0);

glColor3f(0, 1, 0);
glVertex3f(0, 1, 0);
glVertex3f(0, 1, 1);
glVertex3f(1, 1, 1);
glVertex3f(1, 1, 0);

glEnd();

A számábrázolásból adódóan közel azonos Z értékekre „érdekes” megjelenítést kaphatunk:

\(\rhd\) Állítsuk át az előző példát, hogy közel egymáson legyenek a négyzetek, és nézzük meg az eredményt!

glBegin(GL_QUADS);

glColor3f(1, 0, 0);
glVertex3f(0, 0, 0);
glVertex3f(0, 0, 1);
glVertex3f(1, 0, 1);
glVertex3f(1, 0, 0);

glColor3f(0, 1, 0);
glVertex3f(0, 1e-5, 0);
glVertex3f(0, 0, 1);
glVertex3f(1, 0, 1);
glVertex3f(1, 0, 0);

glEnd();

Hátsó lapok eldobása

A megjelenített objektumokat gyakran 3 dimenziós testeknek nevezzük, de technikailag általában csak a felületükkel szoktunk foglalkozni (mivel ez az, amivel a fény kölcsönhatásba lép). Mivel a hátsó lapok egy alakzatnál nem látszódnak, ezért megtehetjük, hogy nem próbáljuk meg megjeleníteni azokat.

Egy lapról úgy tudjuk eldönteni, hogy az elülső, vagy hátsó lap, hogy megnézzük, hogy a felületi normálisa milyen szöget zár be a kamera nézőpontjával.

Mivel egy nagyon egyszerű feltételről van szó, ezért triviális lapeldobásként szoktunk rá hivatkozni.

OpenGL-ben a következőképpen lehet bekapcsolni:

glEnable(GL_CULL_FACE);

Be lehet állítani, hogy az elülső, vagy a hátsó lapok kerüljenek-e eldobásra.

glCullFace(GL_FRONT);
glCullFace(GL_BACK);

Félig átlátszó felületek megjelenítése

A Z-buffer használata abból a feltételezésből indul ki, hogy a közelebb lévő pontok eltakarják a hátrébb lévőket. Hogy ha átlátszó felületrészekkel, vagy félig átlátszó felületekkel dolgozunk, akkor ez nem teljesül.

Dupla bufferelés, tripla bufferelés

Alapvetően az alakzatok (többségében háromszögek) kirajzolása szekvenciálisan, sorrendben történik. A megjelenítendő kép létrehozása közben lévő tranziens állapotokat viszont általában nem szeretnénk látni.

A dupla bufferelés azt feltételezi, hogy van egy megjelenített (front buffer) és egy rejtett (back buffer) képbufferünk.

Az algoritmusa egyszerűen a következő:

  • Rajzoljunk a rejtett bufferbe.

  • Amikor elkészült a megjelenítendő kép, akkor cseréljük meg a rejtett és a megjelenített buffereket.

Az utóbbi tipikusan jelentheti akár csak egy mutató átállítását. Általában az ehhez tartozó függvény neve tartalmazza a swap szót, például SwapBuffer.

A tripla bufferelés akkor lehet szükséges, hogy ha a videókártyáról a kép másolása várni kellene arra, hogy a következő kép összeállítása megkezdődhessen.

\(\rhd\) Ábrázoljuk, hogy milyen három fázisa van a tripla bufferelésnek!

Modellformátumok

Wavefront OBJ

Egy háromszög paraméterei:

f v1/vt1/vn1 v2/vt2/vn2 v3/vt3/vn3

\(\rhd\) Nézzünk bele néhány .obj kiterjesztésű modellfájlba!

STL formátum

solid dart
  facet normal 0 1 0
    outer loop
      vertex 3 1 2
      vertex 2 0 -1
      vertex 8 4 2
    endloop
  endfacet
  facet normal 0 0 1
    outer loop
      vertex 3 9 -10
      vertex 5 1 3
      vertex 4 7 -2
    endloop
  endfacet
endsolid

3DS formátum

Kérdések

  • Milyen fő transzformációk tartoznak a megjelenítési folyamathoz?

  • Mit nevezünk láthatósági problémának?

  • Hogyan működik a festő algoritmus?

  • Például milyen esetet nem képes megoldani a festő algoritmus?

  • Mire szolgál a mélységbuffer és hogyan működik?

  • Mire szolgál a hátsó lapok eldobása, és hogyan működik a módszer?

  • Miért van szükség dupla bufferelésre?

  • Hogyan működik a dupla bufferelés?

  • Milyen előnyei és hátrányai vannak az adatok bináris és a szöveges fájlokban történő tárolásának?

  • A modellekhez milyen adatok tartoznak, amelyeket az OBJ fájlokban tárolunk?

  • Milyen módon tárolja az Wavefront OBJ szabványa a modellekhez tartozó adatokat?

  • Egy betöltött modellt meg tudunk-e jeleníteni több különböző helyen a virtuális terünkben?

  • Hogyan néz ki egy tetraéder adatait tartalmazó OBJ fájl?

  • Mennyi számértéket fog tartalmazni egy szabályos oktaéder adatait tartalmazó OBJ fájl?

  • Hogyan tárolja az OBJ fájl magukat a textúrákat?

  • Miért előnyös, hogy ha a normálvektorok le vannak tárolva a modellfájlban?

Számítási feladatok

  • Tegyük fel, hogy egy \(1024 \times 768\) felbontású képet szeretnénk megjeleníteni! A mélységbufferünkben a távolságok számításához használjunk dupla pontosságú lebegőpontos számokat. Mennyi helyet foglal így a mélységbuffer?

Programozási feladatok

Origin

Töltsük le és nézzük át a origin példát az me-courses repository-ból, majd végezzük el az alábbi módosításokat!

  • Oldjuk meg, hogy a kamerát függőlegesen is lehessen mozgatni felfelé és lefelé q és e billentyűk segítségével!

  • Állítsuk be a j és l billentyűkre a kamera balra és jobbra forgatását!

  • Az egységkockán belül jelenítsünk meg egy színes háromszöget, melynek sárga, cián és magenta színűek a sarkai!

  • Jelenítsünk meg egy szürke (tesszellált) gömböt az egységkockán belül!

  • Válasszuk kicsire a tesszelláció mértékét, és forgassuk meg a gömböt egyenletes sebességgel valamelyik tengely körül!

  • Írjuk át a kamera kezelését úgy, hogy a Google Maps-hez hasonlóan lehessen forgatni a nézetet!

  • Rajzoljunk ki egy sakktábla mintát az egységkockánk x-y síkjába (ahol z értéke 0)!

  • Rajzoljuk ki egy henger és egy kúp közelítését! Használjuk hozzá a triangle strip és triangle fan primitíveket!