4. Térbeli alakzatok leképzése síkra

Az alapvető célunk jelen esetben: térbeli objektumok ábrázolása síkon.

• Jellemzően a 3 dimenziós teret képezzük le 2 dimenziósra.

• Ezt a transzformációt szokták nézeti transzformációnak nevezni.

• A vetítés egy dimenzióvesztő leképzés.

• Elvész a mélységinformáció.

• A vetített képből nem tudjuk teljesen rekonstruálni az eredeti térbeli objektumot.

• https://en.wikipedia.org/wiki/3D_projection

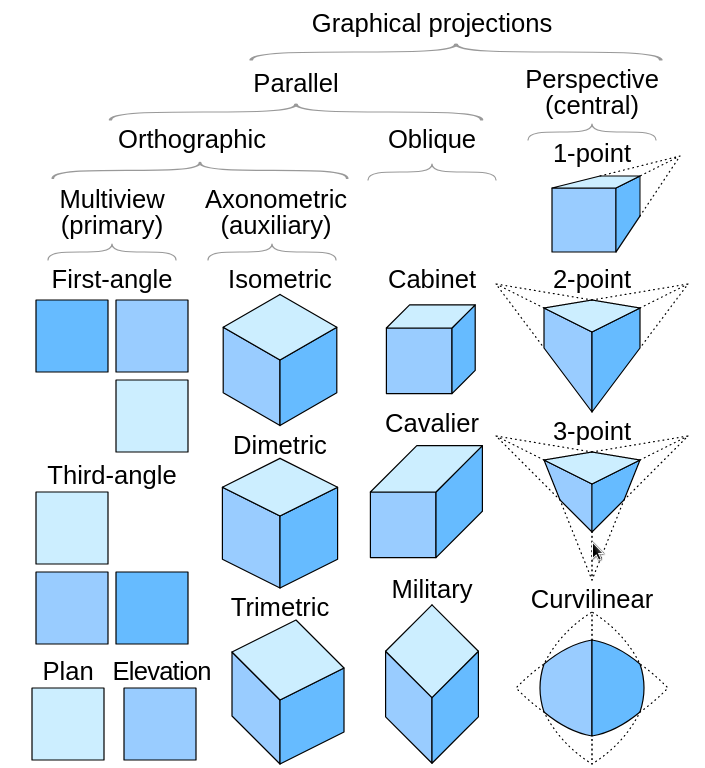
Párhuzamos vetítés

A tér pontjait párhuzamos fénysugarak segítségével vetítjük egy síkra.

• Az eredetileg párhuzamosok a vetítést követően is párhuzamosok maradnak.

• Az arányokat nem feltétlenül tartja meg.

• A kép egészét nézve azt mondhatjuk, hogy a kameránknak tulajdonképpen nincs pozíciója. (Azt végtelenül távolinak tekinthetjük.)

• A világ és a képi koordinátarendszert tekintve értelmezhetjük a kameránk pozícióját.

Orthogonális vetítés

• Merőleges vetítés, orthografikus projekció, analemma

• A párhuzamos vetítés egy alapesete.

• Izometrikus megjelenítés. (A játékok esetében azt is gyakran így nevezik, ahol az élek nem \(120^\circ\) szöget zárnak be.)

• Két és fél 3D

• https://en.wikipedia.org/wiki/Oblique_projection

• https://en.wikipedia.org/wiki/Isometric_video_game_graphics

• https://rocketbrush.com/blog/isometric-games-how-isometry-benefits-game-developers

\[\begin{split}P = \begin{bmatrix} 1 & 0 & \dfrac{1}{2}\cos \alpha \\ 0 & 1 & \dfrac{1}{2}\sin \alpha \\ 0 & 0 & 0 \\ \end{bmatrix}.\end{split}\]

Az \(\alpha\) azt a szöget adja meg, amellyel a \(z\) tengely irányú eltérést szemléltetjük.

Az \((x, y)\) síkra történő vetítés homogén koordinátákkal az alábbi mátrixszal is felírható:

\[\begin{split}P = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}.\end{split}\]

Ez tulajdonképpen a \(z\) tengely szerinti értékek elhagyását jelenti.

Perspektivikus vetítés

• Egy, két és három pontos perspektíva.

• Középpontos vetítés.

• A vetítés középpontjának a szempozíciót tekintjük.

\(\rhd\) Rajzoljunk fel egy kockát egy, két és három pontos perspektivikus ábrázolással!

Megjegyzés

A valódi kamerákhoz képest az egyik eltérés, hogy általában nem vesszük figyelembe a lencsék torzítását.

A vetítési mód vizsgálatához feltételezzük a következőket!

• Egy \((e_x, e_y, e_z)\) pontból szemléljük a teret.

• A tér pontjait az \(z\) tengelyre merőleges síkra szeretnénk vetíteni.

Ezen belül további, két egyszerű esetet is meg tudunk különböztetni.

• Amennyiben feltételezzük, hogy a szempozíciónk az origóban van, és a képernyő síkja a szemtől \(d\) távolságra van, akkor a tér pontjait erre a síkra az alábbi formában vetíthetjük:

\[x' = x \cdot \dfrac{d}{z}, \quad y' = y \cdot \dfrac{d}{z}.\]

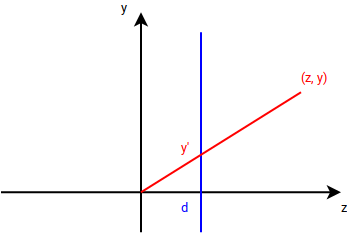
• Hogy ha azt feltételezzük, hogy a képernyő síkja tartalmazza az origót, a szempozíciónk mögötte, a \((0, 0, -e_z)\) pontban van, akkor a számítás a következő:

\[x' = x \cdot \dfrac{-e_z}{z - e_z}, \quad y' = y \cdot \dfrac{-e_z}{z - e_z}.\]

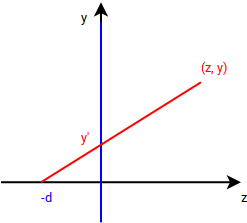
Hogy ha ugyanezt szempozíció helyett a képernyő síkjától való távolsággal adjuk meg, akkor a következőt kapjuk:

\[x' = x \cdot \dfrac{d}{d + z}, \quad y' = y \cdot \dfrac{d}{d + z}.\]

OpenGL

• Open Graphics Library

• Khronos Group

• 1997-ben jelent meg az 1.1-es változata

• https://en.wikipedia.org/wiki/OpenGL

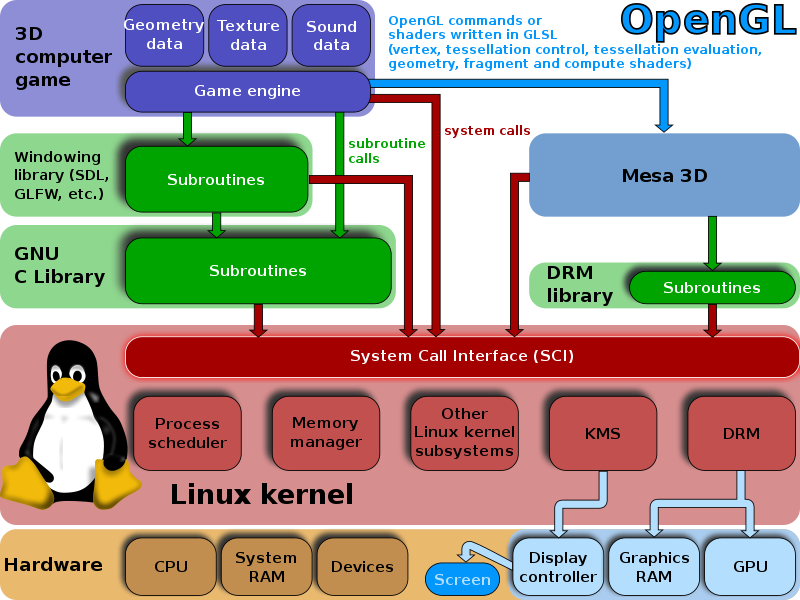
• Az API-ban jellegzetesen gl prefixszel kezdődnek az OpenGL specifikus függvények.

• Egy állapotgépről van szó.

\(\rhd\) Tekintsük át a gl.h fejléc állományt!

\(\rhd\) Milyen alternatívái vannak az OpenGL-nek?

Grafikus alapelemek

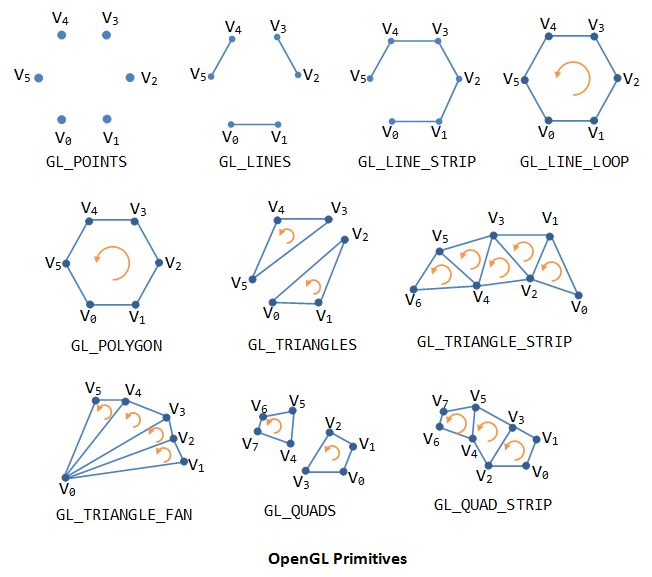
\(\rhd\) Nézzünk meg példákat az egyes alapelemek használatára!

\(\rhd\) Hogyan jeleníthetünk meg kúpot, hengert vagy gömböt?

\(\rhd\) Rajzoltassuk ki egy kocka éleit az alábbi kódrésszel!

glBegin(GL_LINES);
glColor3f(1, 1, 1);

glVertex3f(-1, -1, -1);
glVertex3f(1, -1, -1);
glVertex3f(1, -1, -1);
glVertex3f(1, 1, -1);
glVertex3f(1, 1, -1);
glVertex3f(-1, 1, -1);
glVertex3f(-1, 1, -1);
glVertex3f(-1, -1, -1);

glVertex3f(-1, -1, 1);
glVertex3f(1, -1, 1);
glVertex3f(1, -1, 1);
glVertex3f(1, 1, 1);
glVertex3f(1, 1, 1);
glVertex3f(-1, 1, 1);
glVertex3f(-1, 1, 1);
glVertex3f(-1, -1, 1);

glVertex3f(-1, -1, -1);
glVertex3f(-1, -1, 1);
glVertex3f(-1, 1, -1);
glVertex3f(-1, 1, 1);
glVertex3f(1, 1, -1);
glVertex3f(1, 1, 1);
glVertex3f(1, -1, -1);
glVertex3f(1, -1, 1);

glEnd();

Megjegyzés

A vonalak vastagsága a glLineWidth függvény segítségével beállítható. (https://registry.khronos.org/OpenGL-Refpages/gl4/html/glLineWidth.xhtml)

A leképzett térrész

• A téglalap alakú képernyőnkre, elülső és hátsó vágósík használatával (jellemzően) a tér egy téglalap vagy csonka gúla alakú részét tudjuk leképezni.

• A térrész leírásához a bal, jobb, alsó, felső, elülső és hátsó értékek megadása szükséges.

Orthogonális leképzés

Orthogonális leképzéshez a glOrtho függvényt használhatjuk.

• A megjelenített térrész egy téglalapon belül van.

• https://registry.khronos.org/OpenGL-Refpages/gl2.1/xhtml/glOrtho.xml

void glOrtho(
  GLdouble left,
  GLdouble right,
  GLdouble bottom,
  GLdouble top,
  GLdouble near,
  GLdouble far
);

A transzformáció leírásához vezessük be a következő jelöléseket:

• \(l\): A képtér bal (left) oldala.

• \(r\): A képtér jobb (right) oldala.

• \(t\): A képtér felső (top) oldala.

• \(b\): A képtér alsó (bottom) oldala.

• \(n\): A nézőpont távolsága az elülső (near) vagósíktól.

• \(f\): A nézőpont távolsága a hátsó (far) vagósíktól.

A transzformáció a következő transzformációs mátrixszal írható le:

\[\begin{split}P = \begin{bmatrix} \dfrac{2}{r-l} & 0 & 0 & t_x \\ 0 & \dfrac{2}{t-b} & 0 & t_y \\ 0 & 0 & \dfrac{-2}{f-n} & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix},\end{split}\]

ahol

\[t_x = \dfrac{r+l}{r-l}, \quad t_y = \dfrac{t+b}{t-b}, \quad t_z = \dfrac{f+n}{f-n}.\]

\(\rhd\) Vizsgáljuk meg a glOrtho függvény használatát a Pong példa esetében!

Perspektív leképzés

Perspektivikus leképzéshez a glFrustum függvényt használhatjuk.

• A megjelenített térrész egy csonka gúla. Ezt nevezzük nézeti gúlának.

• https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/opengl-perspective-projection-matrix.html

• https://registry.khronos.org/OpenGL-Refpages/gl2.1/xhtml/glFrustum.xml

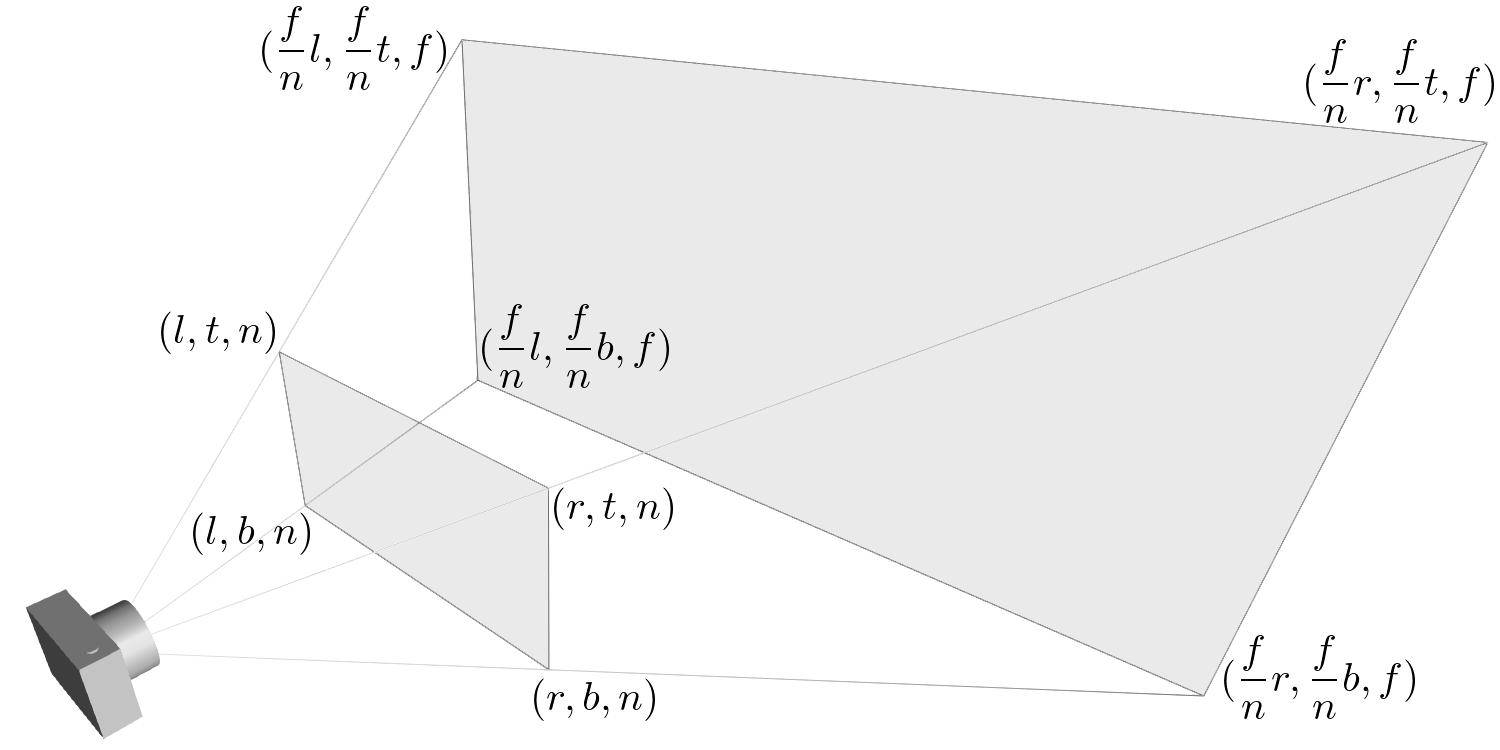
forrás: https://www.songho.ca/opengl/gl_transform.html

A transzformáció mátrixa:

\[\begin{split}P = \begin{bmatrix} \dfrac{2n}{r-l} & 0 & \dfrac{r+l}{r-l} & 0 \\ 0 & \dfrac{2n}{t-b} & \dfrac{t+b}{t-b} & 0 \\ 0 & 0 & -\dfrac{f+n}{f-n} & -\dfrac{2fn}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}.\end{split}\]

Kamera implementálása

Objektum orientált szemlélet szerint a kamerát is egy különálló, nevesített elemnek tekinthetjük.

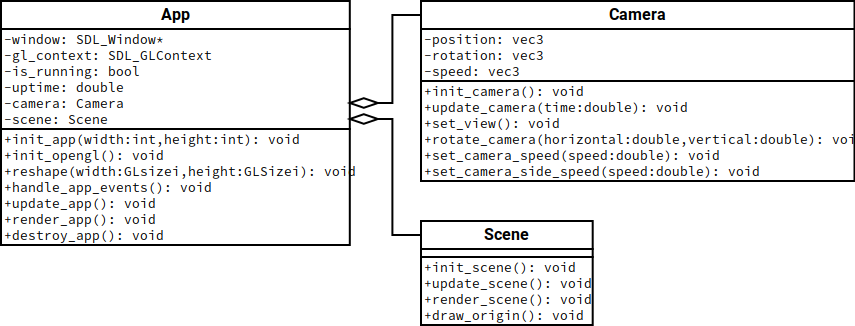
\(\rhd\) Vizsgáljuk meg, hogy hogyan tudjuk mozgatni a kamerát a térben!

Kérdések

• Milyen grafikus alapelemeket képes megjeleníteni az OpenGL?

• Mi a menete egy háromszög megjelenítésének programkód szintjén (az aktuálisan használt változatban/példaprogramokban)?

• Hogyan tudunk gömböt, hengert és kúpot megjeleníteni OpenGL segítségével?

• Hogyan oldjuk meg a kamera kezelését?

Számítási feladatok

1. Tegyük fel, hogy orthogonálisan szeretnénk vetíteni az \((x, z)\) síkra. A szempozíciónk a \((3, 5, 7)\) pontban van. Írja fel a vetítéshez tartozó mátrixot!

2. Orthogonális vetítést feltételezünk. A térbeli \((7, -1, 2)\) pontot az \(x = 6, z = 3\) pontra vetítettük le. Melyik síkra történt a vetítés? Hol volt a szempozíciónk a térben?

3. Adott a \((2, -8, 10)\) pont a térben. Perspektivikus leképzést feltételezve hova kerül a síkon, hogy ha a szempozíciónk az origó, és a képernyősík attól 3 egység távolságra van?

4. Perspektív transzformációval a \((2, -8, 10)\) pontot a \((0.2, -0.8)\) pontba képeztük le. Milyen messze van a szempozíciónk a képernyő síkjától?

Programozási feladatok

Pong

• Nézzük át a pong példát az me-courses repository-ból!

• Változtassuk meg a labda sebességét!

• Javítsuk ki a programot, hogy csak akkor ütközzön vissza a labda bal és jobb oldalt, ha ott van az ütő alatta!

• Kattintással lehessen áthelyezni a labdát!

• Billentyűk segítségével lehessen változtatni a labda méretét bizonyos határokon belül!

• Oldjuk meg, hogy forogjon is a labda egyenletes sebességgel! Ütközés esetén ez a sebesség változzon (például attól függően, hogy melyik oldalnak vagy milyen irányból ütközött neki)!

• Készítsünk két számlálót, amelyik nyilvántartja, hogy melyik játékosnak mennyi pontja van. Ezt valahogyan jelenítsük meg!