6. Fények, árnyalás

A megjelenítendő felületi pontok esetében meg kell határozni a kirajzolás színét. Ezek lehetőségeit, az anyagjellemzők és fényhatások beállításait vizsgáljuk a következőkben.

• https://teaching.csse.uwa.edu.au/units/CITS3003/lectures/017_Shading_in_OpenGL.pdf

• https://opengl-notes.readthedocs.io/en/latest/topics/lighting/shading.html

Egyszerű megjelenítési módok

Rácsvonalak rajzolása

Az OpenGL-ben be lehet állítani, hogy a sokszögeket hogyan rajzoltassa ki.

glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);

\(\rhd\) Nézzük meg a shading nevű példában ennek a hatását!

Megjegyzés

A látványosabb eredményhez célszerű a glClearColor(1, 1, 1, 1); parancsot is kiadni.

Saját színnel való kitöltés

Minden háromszöget a saját színével rajzoltatunk ki. Nem vesszük figyelembe a fényhatásokat.

Ilyen megjelenítést kapunk, hogy ha kikapcsoljuk a fényeket és a textúrázást.

\(\rhd\) Nézzük meg a shading példát!

Árnyalás

BRDF modell

• Árnyalás (shading), anyagjellemző (material)

• Nézőpont, fényforrás iránya, felületi normális

• A modell egy gömbfelület eloszlás formájában adja meg a fény mennyiségét. (Az \(f\) egy sűrűségfüggvényt jelöl.)

• Különféle modelleket adtak a problémára, amellyek részben kombinálhatóak is egymással.

• BRDF: Bidirectional Reflectance Distribution Function

• https://en.wikipedia.org/wiki/Bidirectional_reflectance_distribution_function

Konstans árnyalás

Angolul Flat shading-nek nevezik. OpenGL-ben közvetlenül beállítható:

glShadeModel(GL_FLAT);

\(\rhd\) Forgassuk egyenletes (például 10 fok/másodperc) sebességgel a modellt az \(x\) tengely körül!

Gourand

• A háromszögek csúcspontjaiban számítjuk a normálvektorokkal a színt.

• A csúcspontok színét interpoláljuk a többi pontra.

• https://en.wikipedia.org/wiki/Gouraud_shading

glShadeModel(GL_SMOOTH);

Példa

Adott egy háromszög, mely 3 csúcspontjának a színe \(\textbf{c}_1 = (0.2, 0.7, 0.1)\), \(\textbf{c}_2 = (0, 0, 1)\) és \(\textbf{c}_3 = (0.4, 1, 0.5)\). Számítsuk ki Gourand árnyalás esetén az \(s = 0.4, t = 0.6\) ponthoz tartozó színt!

Phong

• https://en.wikipedia.org/wiki/Phong_shading

A sarokpontokhoz tartozó színek interpolálása helyett

• a normálvektorokat interpoláljuk minden pontra.

• Pontonként vesszük figyelembe a fény hatását.

Szokták még per-fragment shading-nek, vagy per-fragment lighting-nak is nevezni.

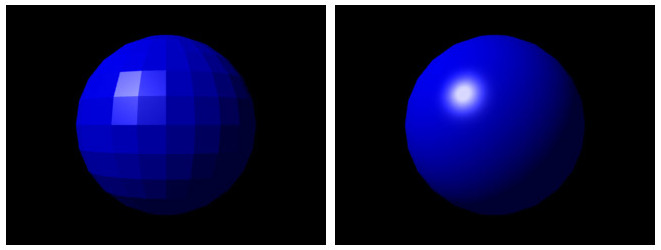
Megjegyzés

Ezt az árnyalási módot az aktuálisan használt OpenGL verziónk nem támogatja.

• https://www.cs.toronto.edu/~jacobson/phong-demo/

Példa

Adott egy háromszög, amelynek normálvektorai \(\textbf{n}_1 = (-2, 4, 1)\), \(\textbf{n}_2 = (-1, 3, 0)\) és \(\textbf{n}_3 = (0, 2, 1)\). Számítsuk ki Phong modell szerint az \(s = 0.5, t = 0.1\) ponthoz tartozó normálvektort!

Fények, anyagjellemzők

A fény fizikai modelljének számítása túlságosan költséges lenne, ezért az OpenGL egy egyszerűbb, praktikusabb modellt használ.

A modell szimmetrikus olyan tekintetben, hogy a fényeket és az anyagjellemzőket ugyanolyan összetevők szerint tudjuk beállítani.

• https://learnopengl.com/Lighting/Basic-Lighting

Az \(\textbf{I}_l\) jelölje a fény intenzitását!

Megjegyzés

Definiáljuk a \(*\) műveletet, amely két, azonos elemszámú vektor elemenkénti szorzatát jelenti!

Környezeti fény

• Szokták ambiens fényösszetevőnek is nevezni.

• A környezetben mindenhol jelenlévő fénynek tekintjük.

• Nem hat rá sem a fényforrás, sem a nézőpont pozíciója.

\[\textbf{A} = \textbf{k}_a * \textbf{I}_a,\]

ahol

• \(\textbf{I}_a\): a környezeti fény,

• \(\textbf{k}_a \in [0, 1]^3\): a felület környezeti fény visszaverződési állandója.

Példa

Egy teljesen sárga színű fénnyel világítunk meg egy felületi pontot, melynél a környezeti fény visszaverődési állandók \((0.2, 0.9, 0.3)\). Milyen lesz a visszaverődő környezeti fény színe?

Szórt fény

• Szokták diffúz fényösszetevőnek is nevezni.

• Csak a fényforrás pozíciója befolyásolja, a nézőpont nem.

\[\textbf{D} = \textbf{k}_d * \textbf{I}_d \cdot \cos \theta, \quad \cos \theta = \dfrac{\textbf{l} \cdot \textbf{n}}{|\textbf{l}| \cdot |\textbf{n}|},\]

ahol

• \(\textbf{I}_d\): a szórt fényösszetevő,

• \(\textbf{k}_d \in [0, 1]^3\): a felület szórt fény visszaverződési állandója,

• \(\theta \in \left[0, \dfrac{\pi}{2}\right]\): a fénysugár felületi normálissal bezárt szöge,

• \(\textbf{n}\): a felületi normális,

• \(\textbf{l}\): a felületi pontból a fényforrásba mutató vektor.

Példa

Teljesen türkizkék szórt fénnyel világítunk meg egy felületet, amelynél az anyag szórt fényösszetevője \((0.9, 0.3, 0.4)\). A felületi normális a fény irányával \(60^{\circ}\)-os szöget zár be. Milyen lesz a visszaverődő szórt fény?

Tükröződő fény

• Szokták spekuláris fényösszetevőnek is nevezni.

• A fényforrás és a nézőpont pozíciója egyaránt számít.

• https://registry.khronos.org/OpenGL-Refpages/gl2.1/xhtml/glColorMaterial.xml

• https://registry.khronos.org/OpenGL-Refpages/gl2.1/xhtml/glLight.xml

A tükröződő fény akkor lehet nem 0, hogy ha értelmezhető a felületről visszaverődő fény, vagyis \(\textbf{l} \cdot \textbf{n} > 0\). Ekkor

\[\textbf{S} = \max \left( \left(\dfrac{\textbf{s} \cdot \textbf{n}}{|\textbf{s}| \cdot |\textbf{n}|}\right)^e, 0 \right) \textbf{I}_s * \textbf{k}_s, \quad \textbf{s} = \dfrac{\textbf{l}}{|\textbf{l}|} + \dfrac{\textbf{v}}{|\textbf{v}|},\]

ahol

• \(\textbf{I}_s\): a tükröződő fényösszetevő,

• \(\textbf{k}_s \in [0, 1]^3\): a felület tükröződő fény visszaverződési állandója,

• \(e \in \mathbb{R}\): az anyag ragyogási összetevője.

Fény tompítása

• Azt írja le, hogy a fény erőssége a távolság függvényében hogyan változik.

• Angolul attenuation-ként emlegetik.

\[f_{\text{att}} = \min\left( \dfrac{1}{c_0 + c_1 \cdot d + c_2 \cdot d^2}, 1 \right),\]

ahol

• \(d\): a felületi pont fényforrástól való távolsága,

• \(c_0, c_1, c_2\): a tompításra jellemző valós konstansok.

Példa

Egy felületi pont fényforrástól való távolsága 10 egység. A fény tompítását a \(c_0 = 0.5, c_1 = 0, c_2 = 0.3\) paraméterekkel írjuk le. Mennyi lesz a fény tompítása?

Több fényforrás

Több fényforrás esetében az alábbi összefüggéssel számolhatunk:

\[\textbf{I} = \textbf{I}_e + \textbf{I}_g * \textbf{k}_a + \sum_{i=1}^n T_i(\textbf{A}_i + \textbf{D}_i + \textbf{S}_i),\]

ahol

• \(\textbf{I}_e\): a felület által kibocsájtott (emisszív) fény,

• \(\textbf{I}_g\): a globális környezeti fény,

• \(\textbf{k}_a\): a felület ambiens együtthatója,

• \(T_i\): az \(i\)-edik fényforrás tompítási tényezője (attenuation),

• \(\textbf{A}_i\): az \(i\)-edik fényforrás ambiens értéke,

• \(\textbf{D}_i\): az \(i\)-edik fényforrás diffúz értéke,

• \(\textbf{S}_i\): az \(i\)-edik fényforrás spekuláris értéke.

Speciális fényhatások

Szpotlámpa

Szpotlámpaszerű fényhatást is be tudunk állítani. Ehhez meg kell adnunk

• a világítás irányát (GL_SPOT_DIRECTION),

• a lámpa világításának szögét (GL_SPOT_CUTOFF),

• a fény eloszlását, sűrűségét (GL_SPOT_EXPONENT \(\in [0, 128]\), ahol 0 az egyenletes, a 128 a leginkább fókuszált).

float direction[] = {0.0, 0.0, -1.0, 1.0};
glLightfv(GL_LIGHT0, GL_SPOT_DIRECTION, direction);
glLightf(GL_LIGHT0, GL_SPOT_CUTOFF, 30.0);
glLightf(GL_LIGHT0, GL_SPOT_EXPONENT, 10.0f);

\(\rhd\) Jelenítsünk meg egy \(10 \times 10\) méretű négyzetet, és világítsuk meg szpotlámpával!

glPushMatrix();
glScalef(10, 10, 1);
draw_plane(50);
glPopMatrix();

Köd

• https://www.mbsoftworks.sk/tutorials/opengl4/020-fog/

• https://opengl-notes.readthedocs.io/en/latest/topics/texturing/aliasing.html

• https://registry.khronos.org/OpenGL-Refpages/gl2.1/xhtml/glFog.xml

A ködöt egyszerűen a glEnable(GL_FOG) paranccsal lehet bekapcsolni.

glEnable(GL_FOG);
float fog_color[] = {1, 1, 1, 1};
glFogfv(GL_FOG_COLOR, fog_color);

Kérdések

• Melyek az alapszínek additív és szubtraktív színkeverés esetén?

• A fényeket az OpenGL milyen alapvető összetevőkre bontja?

• Ha egy magenta színű labdát ciánkék színnel világítunk meg, akkor az milyennek fog látszani?

• Ha egy zöld labdát sárga színű fénnyel világítunk meg, akkor az milyennek fog látszani?

• Ha egy fehér objektumot egyidejűleg világítunk meg sárga és kék színű fénnyel, akkor az milyennek fog látszani?

• Mi az alapvető különbség a szórt (diffúz) és a spekuláris fény között?

• Az OpenGL lehetővé teszi-e azt, hogy egy objektum fekete színben „csillogjon”?

• OpenGL-ben hogyan tudjuk szabályozni a fényerőt?

• Milyen esetben számít OpenGL-ben a fényforrás pozíciója?

Számítási feladatok

• Adott egy háromszög, mely 3 csúcspontjának a színe \(\textbf{c}_1 = (0.3, 0.2, 0.9)\), \(\textbf{c}_2 = (0, 1, 0)\) és \(\textbf{c}_3 = (0.5, 0, 0.5)\). Számítsuk ki Gourand árnyalás esetén az \(s = 0.1, t = 0.2\) ponthoz tartozó színt!

• Adott egy háromszög, amelynek normálvektorai \(\textbf{n}_1 = (-3, 4, -1)\), \(\textbf{n}_2 = (0, 3, 2)\) és \(\textbf{n}_3 = (0, 2, 2)\). Számítsuk ki Phong modell szerint az \(s = 0.3, t = 0.7\) ponthoz tartozó normálvektort!

• Egy teljesen zöld színű fénnyel világítunk meg egy felületi pontot, melynél a környezeti fény visszaverődési állandók \((0.2, 0.9, 0.3)\). Milyen lesz a visszaverődő környezeti fény színe?

• Teljesen türkizkék szórt fénnyel világítunk meg egy felületet, amelynél az anyag szórt fényösszetevője \((0.1, 0.2, 0.8)\). A felületi normális a fény irányával \(45^{\circ}\)-os szöget zár be. Milyen lesz a visszaverődő szórt fény?

• Egy felületi pont fényforrástól való távolsága 5 egység. A fény tompítását a \(c_0 = 0.6, c_1 = 0.1, c_2 = 0\) paraméterekkel írjuk le. Mennyi lesz a fény tompítása?

Programozási feladatok

OBJ loader statikus library használata

• Keressük meg az me-courses repository-ban a utils nevű mappát!

• A statikus library a utils/obj jegyzékben van.

• Lépjünk be a jegyzékbe, és adjuk ki a make parancsot.

• Létre fog jönni egy libobj.a fájl. Ezt másoljuk be a fordító lib jegyzékébe.

• A utils/obj/include jegyzékben lévő header fájlokat másoljuk be a fordító include/obj nevű jegyzékébe. (Az obj nevű jegyzék nem létezik, azt létre kell hozni.)

Blender

• A modellek szerkesztéséhez Blender-t érdemes használni: https://www.blender.org/

• A modell exportálásánál figyelni kell arra, hogy

  • a modell csak háromszögeket tartalmazzon (Triangle faces kapcsoló),

  • a felfele irány megfelelően legyen megadva (általában Z szokott lenni),

  • a modell a normálvektorokat és a textúrakoordinátákat is tartalmazza (ez alapértelmezés szerint jól van),

  • csak a kijelölt vagy az összes objektumot el kell-e menteni (részemről inkább a kijelöltre hagyatkozom).

• A modellek előkészítéséről és használatáról itt található egy videó: https://www.uni-miskolc.hu/~matip/_downloads/grafika/animals.ogv

Cube

• Fordítsuk le és futtassuk a cube nevű példaprogramot!

• Próbáljuk kicserélni benne a modellt!

• Rajzoljuk ki ugyanazt a modellt egy 4x4-es rácsba!

• Töltsünk be egyszerre két modellt, és az egyiket forgassuk!

• Töltsünk be egyszerre két modellt, és az egyiket lehessen mozgatni egér és/vagy billentyűk segítségével!

• Próbáljuk meg betölteni és megjeleníteni a https://www.uni-miskolc.hu/~matip/_downloads/grafika címre feltöltött modelleket!

• Nézzük meg, hogy a modell adatai hogyan kerülnek tárolásra az OBJ fájlokban!

• Módosítsuk a megjelenített modell színét és pozícióját!

• Töltsük be és jelenítsük meg egyszerre a kocka és a ház modelljét!

Fények

• Töltsük le és futtassuk a cube nevű példát!

• Állítsuk be a fény és az anyagtulajdonságok összetevőit úgy, hogy csak egy-egy összetevő nem nulla!

• Próbáljuk ki a fényösszetevők kombinációit!

• Töltsünk le további modelleket a https://www.uni-miskolc.hu/~matip/_downloads/grafika oldalról és jelenítsük meg ezeket!

• Méretezzük és helyezzük el ezeket megfelelően!

• Forgassuk egyenletes sebességgel a modelleket idő függvényében!

• Állítsuk be az anyagjellemzőket úgy, hogy a modellek fémes hatásúak legyenek!

• Mozgassuk a fényforrást!

• Oldjuk meg, hogy lehessen változtatni a fényerősséget billentyűk segítségével!

• Változtassuk a fény erősségét/színét idő függvényében!