1.3. A lézerműködés atomfizikai alapjai

1.3.1. Atomok színképe

Izzó gáz vagy gőz spektrális eloszlásfüggvényét (spektrumát) az alábbi kísérleti elrendezésben mérhetjük meg. A kiválasztott fénysugarat a prizma a frekvenciának (hullámhossznak) megfelelően más-más szögben téríti el, amit a (mozgatott) detektorral mérhetünk. A tapasztalat szerint az így felvett emissziós spektrum (színkép) csak néhány frekvenciát tartalmaz, azaz a spektrum - ellentétben az izzó szilárd test folytonos spektrumú sugárzásával – vonalas. (A látható tartományban ténylegesen színes vonalak jelennek meg a detektor helyére tett ernyőn.) A tapasztalat szerint a vonalas spektrum a gáz anyagi minőségétől függ. Molekuláris gázok esetén a színkép bonyolultabb, sávos szerkezetű, de nagyfelbontású műszerekkel látható, hogy a sávok is egymáshoz közel eső vonalakból állnak.

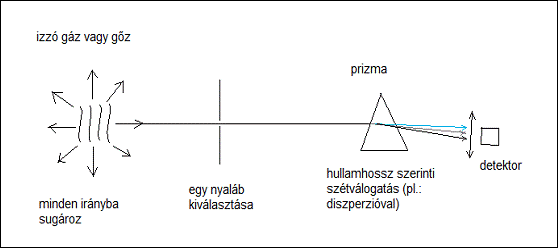
1.3.1.1. ábra: Atomok emissziós spektrumának a felvétele

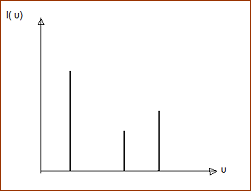
1.3.1.2. ábra: Az atomok emissziós spektruma vonalas

Az izzó szilárd test folytonos spektrumú sugárzását hideg gázon átbocsátva és prizmával felbontva nyerhetjük az abszorpciós spektrumot, ami nem teljesen folytonos, benne fekete vonalak maradnak, az anyagi minőségtől függően. A tapasztalat szerint egy gáz hideg állapotában éppen azokat a vonalakat nyeli el, amelyeket izzó állapotában emittálni tud (Kirchoff-törvény).

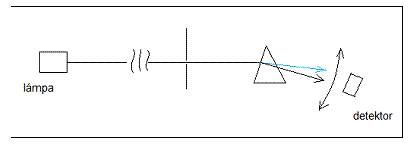
1.3.1.3. ábra: Az abszorpciós spektrum felvétele

Magyarázat a Bohr posztulátumokkal:

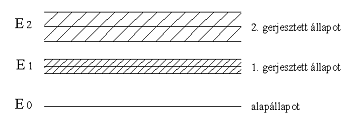
1.) Az atomban az elektronok csak diszkrét E₁, E₂…. energiaszinteken tartózkodhatnak, és ezekben az úgynevezett stacionárius állapotokban tartózkodva nem sugároznak.

2.) Az atomok akkor sugároznak, amikor egy atomi elektron egy magasabb energiájú stacionárius állapotból egy -vel alacsonyabb energiájú állapotba ugrik. Ekkor a kibocsátott frekvencia: , ahol (Planck-állandó). Ezt a képletet Bohr-féle frekvencia feltételnek is nevezik.

Az egyszerűség kedvéért tekintsünk egy olyan atomot, amelynek csak két stacionárius állapota van E₁ és E₂ energiákkal. Az E₁ energiájú állapotot alapállapotnak, a másikat gerjesztett állapotnak nevezzük. Az emittált (kibocsájtott) foton frekvenciája: A Bohr-féle frekvencia feltételt átírhatjuk a formába is. Ez a forma mutatja az emisszió, melynek során tehát az atom gerjesztettsége megszűnik (az atom „legerjed”), energiaviszonyait. Az atom energiája pontosan a sugárzás által elvitt h·f energiával csökken. Ezt az energiadagot, amely a továbbiakban (legalábbis egyes kísérletekben) részecskeként fog viselkedni, fotonnak fogjuk nevezni. Az energia, a fény adagos viselkedéséről a klasszikus elektrodinamika nem tud számot adni, ezt az adagosság fizikája, a kvantummechanika területe.

Az abszorpció során az atom gerjesztett állapotba kerül, energiája pontosan annyival növekszik, amennyivel az emisszió során csökkent. Ezt az energiát csak egy olyan foton tudja átadni az atomnak, amelynek frekvenciája egyezik az emittáltéval. Az alapállapotú atomra beeső fotonok közül csak az tud elnyelődni, amelyiknek a frekvenciája pontosan a fenti érték. A fehér fényből az atom ezt az egy frekvenciát nyeli el, a többi nincs rá hatással.

1.3.2. A kvantummechanikai tárgyalásmód, a határozatlansági reláció

A mikrorendszereket, azaz az atomokat és azok csoportjait (molekulák, kristályok) a kvantummechanika segítségével lehet tárgyalni. Ennek segítségével levezethetők a Bohr-posztulátumok is. Az atomi energiaszintek léte, azok pontos értéke, a közöttük lehetséges átmenetek mind-mind levezethetők a kvantummechanika alapaxiómáiból. A kvantummechanika azonban bonyolult elmélet, tárgyalása meghaladja e jegyzet kereteit. Ezért ebben a jegyzetben az atomfizikai jelenségeket is a klasszikus fizika fogalmai segítségével tárgyaljuk.

Természetesen számos olyan jelenség van, amelyek csupán a klasszikus fizika ismeretében nem érthetünk meg, amelyeknél a kvantummechanika egyes eredményeinek az alkalmazása elkerülhetetlen. A legfontosabb ilyen eredmény a Heisenberg-féle határozatlansági reláció. A reláció szerint az összetartozó (kanonikusan konjugált) fizikai mennyiségek egyszerre nem mérhetők tetszőleges pontossággal, egyidejűleg nem határozhatók meg. Az egyik mennyiség pontos mérése a másikat automatikusan határozatlanná teszi.

Tekintsük például a helykoordinátát (x) és a hozzá tartozó lendület koordinátát (px)! A határozatlansági reláció szerint a helykoordináta bizonytalansága (Δx) és a lendület x koordinátájának bizonytalansága (Δpx) között fennáll a

reláció, ahol h a jól ismert Planck-állandó. Tehát a hely és a lendület egyidejűleg nem mérhető pontosan. Minél pontosabba ismerem a részecske helyét annál kevésbé ismerhetem a lendületét.

Hasonló reláció áll fenn az energia (E) és az időkoordináta (t) között:

Tehát az energia és az időkoordináta sem mérhető egyidejűleg pontosan. Rövid időtartamra az energia nincs pontosan meghatározva. Minél tovább tart a részecske egy állapota (folyamata), annál pontosabban meghatározható (ill. meghatározott) az energiája!

A határozatlansági reláció igen szépen mutatja, hogy a makrofizikai fogalmak a mikrovilág leírására csak korlátozottan alkalmasak. A kapható válasz pontosságát a kísérleti körülmények eleve behatárolják. Egy fizikai mennyiség mérési pontosságának nem lesz elvi határa, ha a kísérleti körülményeket meg tudjuk úgy választani, hogy a mért mennyiség konjugált párja a mérés során határozatlan marad.

Alkalmazások:

p^f_x

1, Fénysugár minimális divergenciája:

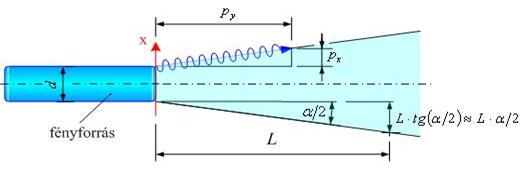
1.3.2.1. ábra: Fényforrásból kilépő fénysugár adatai

èP_f=h/λ (a foton lendülete)

èx: a fotonok x koordinátája (amikor átjönnek a jelzett felületen), a fénysugár irányára merőleges irány

è: a fotonok x irányú lendülete (amikor átjönnek a jelzett felületen)

mert a fotonok a (-d/2, d/2) intervallumon jönnek át

mert az összes foton a megadott kúpon belül halad

, amiből

Tehát például egy λ= 633 nm hullámhosszúságú fénysugár átmérőjének és divergenciájának szorzata nem lehet 2·10^-7 m·rad-nál kisebb. Ha a fénysugár átmérője d= 1mm, akkor az elvileg elérhető minimális nyalábdivergencia 2·10^-4 radián. Ha a fénysugár átmérőjét tízszeresére növeljük, akkor minimális nyalábdivergencia tized részére csökkenthető (lásd a nyalábtágítót!).

2, A másik határozatlansági reláció szerint , amiből

Tehát a kisugárzott frekvencia és a folyamat ideje bizonytalanságainak szorzata 10^-1-nél kisebb nem lehet. A Δt időbizonytalanságot többféleképpen is interpretálhatjuk, attól függően, hogy a kibocsájtás atomi folyamatát, vagy a kialakult fénysugarat tekintjük. A tapasztalat azt mutatja, hogy ezek a nagyon különböző interpretációk egyszerre igazak lehetnek, legalábbis egy kettes-hármas faktor erejéig.

Tekintsük először a kibocsájtás atomi folyamatát. A legalsó szinten az alapállapotban az elektron – külső behatás hiányában – tetszőleges ideig tartózkodhat. Végtelen hosszú tartózkodási idő bizonytalansága is csak végtelen nagy lehet (τ₀ = Δt = ∞), ehhez pedig a határozatlansági reláció alapján pontosan meghatározott energia tartozik (ΔE = Δf = 0).

A gerjesztett állapotokból az elektron előbb-utóbb alacsonyabb energiájú állapotba kerül. A véges időbizonytalanság pedig – a fentiek szerint - az energiaszélességük véges voltát és a spektrumvonalak véges kiszélesedését jelenti. Tipikus a külső atomi héjakra jellemző élettartam τ₁ = 10^-8 s. Ez az adott energiaszint ΔE > 10^-26-10^-27 J kiszélesedését jelenti. Az erről a szintről történő átmenethez tartozó spektrumvonal pedig legalább Δf >10⁷ Hz = 10 MHz szélességű lesz. (Ezek az adatok arra az esetre vonatkoznak, amikor a bomlás stabil szintre történik.)

Egyes gerjesztett állapotokból az alacsonyabb szintekre az elektron sugárzás kibocsájtásával csak hosszabb várakozás után tud lejutni. Az ilyen átmeneteket tiltottaknak nevezzük, mert bizonyos fizikai mennyiségek (pl. perdület) megmaradása az átmenet során csak körülményesen biztosítható. (Tehát a tiltott átmenet is végbemegy, csak sokkal lassabban!) Azt az állapotot, amelyről lefelé minden átmenet tiltott, metastabil állapotnak nevezzük. A metastabil állapototok tipikus élettartama pl. τ₁ = 10^-3 s., amihez Δf > 100 Hz szélességű spektrumvonal tartozik. Tehát ebben az interpretációban a spektrumvonalak szélessége az elbomló állapot élettartamáról árulkodik, szélesebb spektrumvonal rövidebb életidejű gerjesztett állapothoz tartozik.

1.3.2.2. ábra: Atomi energiaszintek és spektrumvonalak kiszélesedése

Amennyiben a kialakult fénysugarat, a fotonfolyamot tekintjük, akkor a Δt az elemi hullámvonulatok lefutásának idejét jelentheti. Mivel a fény sebessége c, az elemi hullámvonulatok hossza L=c·Δt. Mivel a határozatlansági reláció szerint , ezért:

.

Az elemi hullámvonulatok hossza nyilvánvalóan az a legnagyobb optikai útkülönbség, amelynél még lehet interferencia, tehát a koherenciahossz (), tehát a fenti reláció arra is vonatkozik:

Tehát például egy Δf = 100 MHz frekvencia kiszélesedésű fénysugár koherenciahossza legalább 30 cm.

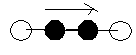
1.3.3. Az indukált emisszió

Einstein jött rá először arra, hogy a fentebb vázolt abszorpció és emisszió mellett kell léteznie egy harmadik elemi atomi folyamatnak, ami indukált emissziónak nevezünk. A folyamat során a gerjesztett atomot olyan frekvenciájú foton éri el, amelyet ő maga is ki tudna bocsátani. A bejövő foton hatására ez a kibocsájtás meg is történik, miközben az atom gerjesztettsége megszűnik. A beérkező (az atom mellett elhaladó) foton tehát egy második foton emisszióját indukálja. A második foton az eredetivel megegyező frekvenciájú, vele azonos irányban halad, fázisuk azonos. Az ilyen tulajdonságú fotonok koherensek.

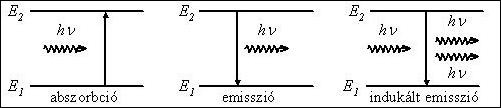
1.3.3. ábra: Elemi atomi fotonos folyamatok

Hogy a két emissziós folyamatot még jobban megkülönböztessük, a magától bekövetkező, eddig csak emissziónak nevezett elemi atomi folyamatot a továbbiakban spontán emissziónak nevezzük. Ez a folyamat tehát csupán az atom energiaminimumra törekvése miatt, magától, minden külső körülménytől függetlenül bekövetkezik, de nem azonnal. A folyamat időigénye, azaz a gerjesztett állapot élettartama tipikusan ~10^-8 s, de ettől jelentős eltérések is lehetnek (az ún. metastabil állapotoké milliószor hosszabb ideig is létezhetnek). Ezzel szemben az indukált emisszió időkésés nélkül, azonnal bekövetkezik.

Most pedig (Einstein nyomán) vizsgáljuk meg a három elemi folyamat bekövetkezésének valószínűségeit!

Az abszorpció során tehát pontosan annyi atom kerül gerjesztett állapotba, mint amennyi foton elnyelődik. Az időegység alatt elnyelt fotonok száma () nyilvánvalóan arányos a beérkező (megfelelő frekvenciájú) fény I(f) intenzitásával és az alapállapotú atomok N1 számával. A folyamat során az alapállapotú atomok száma csökken, ezért előjele negatív: . A B12 állandó jellemző az atomra, az abszorpció Einstein-féle valószínűségi tényezője.

A spontán emisszió nem függ külső körülményektől, tehát a száma csak a gerjesztett állapotú atomok N2 számától függ. Minden spontán emittált foton eggyel növeli az alapállapotú atomok számát, mert közben az atom gerjesztettsége megszűnik. Időegység alatt tehát: . Az A21 mennyiség a spontán emisszió Einstein-féle tényezője.

Az indukált emisszió valószínűsége függ a beérkező (megfelelő frekvenciájú) fény I(f) intenzitásától és a gerjesztett állapotú atomok N2 számától. Az alapállapotú atomok száma az indukált emisszió során is nyilvánvalóan növekszik: . A B21 atomi állandó az indukált emisszió Einstein-féle valószínűségi tényezője.

A továbbiakban tételezzük fel, hogy ezekből a két energiaszinttel rendelkező atomokból nagyon sokat bezárunk egy T hőmérsékletű tartályba (üregbe). A magára hagyott rendszer termikus egyensúlyba kerül. Az üregbe zárt, termikus egyensúlyba került atomokra teljesül, hogy:

1. mind az alap-, mind a gerjesztett állapotú atomok száma állandó:

;

2. jó közelítéssel érvényes a Maxwell-Boltzmann energiaeloszlás[1]:

;

3. az üregben kialakult sugárzás spektrális eloszlását a Planck-törvény írja le:

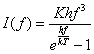
Behelyettesítve az 1.-ban található egyenletbe: ,

majd átrendezve: .

Felhasználva a Maxwell-Boltzmann energiaeloszlás képletét: . Ezt behelyettesítve az előző egyenletbe, majd B₂₁-gyel beosztva:

.

Ebből I(f)-et a Planck-törvénnyel történő összevetés céljából kifejezhetjük: .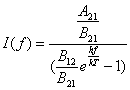

Az összevetés azt eredményezi, hogy

· , azaz a spontán és indukált emisszió valószínűségi tényezőinek az aránya a frekvencia köbével arányos. Az indukált emisszió tehát inkább a kisebb frekvenciákra jellemző.

· , azaz az abszorpció és a spontán emisszió Einstein féle valószínűségi tényezője megegyezik. Tehát egy alapállapotú atom pontosan ugyanakkora valószínűséggel abszorbeál egy fotont, mint amekkora valószínűséggel kényszerít indukált emisszióra egy gerjesztett atomot egy foton.

1.4. Lézerek működési elve, általános felépítésük. A lézerek módusairól.

1.4.1. Lézerek működési elve, a populációinverzió.

A lézer szó az angol LASER szóból származik. Ez utóbbi egy mozaikszó: Light Amplification by the Stimulated Emission of Radiation, ami magyarul azt jelenti, hogy: fényerősítés a sugárzás indukált emissziójával. A lézer működéséhez tehát az szükséges, hogy domináljon az indukált emisszió, és a fény általa erősödjön. Nézzük meg ezeket a feltételeket külön-külön! Először vizsgáljuk meg a spontán módon és indukált emisszióval kibocsájtott fotonok arányát!

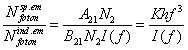
Látható, hogy bármilyen f frekvencián létezik egy I(f) intenzitás, amelynél a kétféle módon kibocsájtott fotonok száma megegyezik. Ennél kisebb intenzitásnál mindig a spontán emisszió, fölötte az indukált emisszió dominál. Ez a kritikus intenzitás azonban a frekvencia köbével arányos. Tehát kis frekvenciákon (pl: mikrohullám) már igen kis intenzitásnál is az indukált emisszió dominál. Nagyobb frekvenciákon (pl. UV sugárzás) azonban a spontán emisszió dominanciája csak igen nagy intenzitásoknál szűnik meg. A képlet alapján megérthetjük azt is, hogy miért a mikrohullámú tartományban működött először az indukált emisszión alapuló erősítés. (A lézerek elődjeinek tekinthető MASER-ek nevének első betűje a mikrohullámra utal.)

Tekintsük most az emittált és abszorbeált fotonok számának arányát!

Van olyan nagy fényintenzitás, amelynél a számláló első tagja elhanyagolható a második mellett, azaz a spontán emisszióval már nem kell számolni. Akkor ez a hányados egyszerűsödik és végeredményben a gerjesztett és az alapállapotú atomok számának az arányához tart. Ha tehát több az alapállapotú atom, mint a gerjesztett, akkor több az abszorpció, mint az emisszió. A fotonok száma fogy, a sugárzás elnyelődik az anyagban. Ha a gerjesztett atomok száma nagyobb, akkor az emisszió meghaladja az abszorpciót, a sugárzás az anyagban erősödik.

Hőmérsékleti egyensúlyban közelítőleg érvényes a Boltzmann-eloszlás, tehát alapállapotban mindig több atom található (N₁ > N₂). Ebben az állapotban – amit normál populációnak nevezhetünk – tehát dominál az abszorpció, a fény az anyagban elnyelődik.

Ha a helyzet fordított, azaz a gerjesztett állapotú atomok vannak többségben (N₁ < N₂), akkor viszont az anyagba belépő sugárzás erősödik. Ilyet a hétköznapi életben nem szoktunk tapasztalni, ez a fordított állapot „magától” nem szokott bekövetkezni. Nagyon különleges anyagokban különleges körülmények között azonban megvalósíthatjuk ezt a fordított populációt, amit szokás populációinverziónak is nevezni. A populációinverzió tehát a sugárzás közegbeli erősödésének alapvető feltétele. (De önmagában ez nem elegendő, hisz kis intenzitásnál a spontán emisszióval is számolni kell.)

A fény a közegben tehát akkor erősödik, ha az emissziók száma meghaladja az abszorpciókét, azaz a nettó emisszió pozitív:

A fotonok száma nyilvánvalóan arányos a fény intenzitásával. A fotonszám (vagy fényintenzitás) növekedését Δt időtartamra vagy az ez alatt a fény által megtett Δx útra is vonatkoztathatjuk. A fényintenzitás egységnyi úton történő növekedése tehát arányos a fény intenzitása mellett a gerjesztett és alapállapotbeli atomok számának a különbségével:

.

A differenciák differenciálokra történő átírása és az átrendezés után kapott differenciálegyenlet:

A differenciálegyenlet megoldása exponenciális függvény lesz, tehát a lézer anyagában megtett útja függvényében a sugárzás exponenciálisan erősödik:

.

(Az erősödés természetesen csak N₂>N₁ esetére (populációinverzió) igaz, N₂<N₁ esetén (normál populáció) a sugárzás a közegben exponenciálisan gyengül.)

Az exponenciális erősödés nem tart a végtelenségig, nagy intenzitásoknál az indukált emisszió lecsökkenti N₂-t. Ez a csökkenés határesetben N₁–ig tarthat, ekkor az indukált emisszió egyensúlyba kerül az abszorpcióval, a sugárzás nem erősödik tovább.

1.4.2. A lézerek négy energiaszintje

A populációinverziót igen nehéz (talán lehetetlen) lenne megvalósítani egy olyan rendszerben, amely csak két energiaszinttel rendelkező atomokból áll.

A lézerműködéshez elengedhetetlenül szükséges populációinverzió csak a termikus egyensúlytól távoli rendszerekben valósulhat meg. Ilyen rendszert csak úgy hozhatunk létre, hogy a rendszerbe folyamatosan energiát táplálunk. A bevitt energiával az atomi elektronokat szelektív módon magasabban gerjesztett állapotokba juttatjuk. Ezek az elektronok aztán egyre kisebb energiájú gerjesztett állapotokon keresztül törekednek az alapállapotba jutni. E folyamat során a hosszabb élettartamú gerjesztett állapotokban (amelyeket metastabil állapotoknak nevezzük) nyilvánvalóan több elektron tartózkodik, mint a rövidebb élettartamúakban. Ha közülük a hosszabb élettartamú nívó van feljebb, akkor a populációinverziót e két szint között máris megvalósítottuk. Ehhez azonban valóságos rendszerekben több energiaszintre is szükség van, a tipikus lézerben minimálisan négy energiaszint van, amelyekhez négy elemi energiaátadó lépés tartozik.

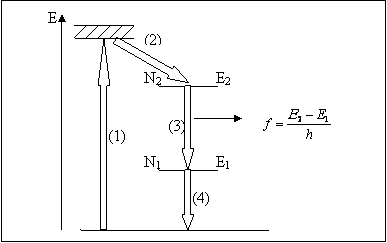
1.4.2. ábra: A lézerek négy energiaszintje és a négy elemi energiaátadó lépés

Az (1) lépésben az atomot valamilyen hatékony és szelektív mechanizmus segítségével egy, a lézernívók fölötti (esetleg azzal egybeeső energiájú) szintre juttatjuk. Erről a szintről (esetleg szintekről) az elektronok igen gyorsan a felső lézerszintre jutnak. Ez a (2) jelű lépés legtöbbször sugárzásmentes átmenet, a közben felszabadult energia a lézeranyagot melegíti. Ezt követi az E₂ és E₁ szintek közötti lézerátmenet (3), amely során a lézerfényt alkotó fotonok egyike is kisugárzódik. A populációinverzió akkor állhat fönn, ha az alsó lézerszint igen gyorsan kiürül (4). Az ilyen típusú energiadiagrammal rendelkező lézereket négyszintű lézereknek nevezzük.

Egyes lézerekben ez (4) lépés hiányozhat (azaz az alsó lézerszint az alapállapot), ekkor a populációinverzió megvalósítása sokkal nehezebb. Ez utóbbi esetben a lézer háromszintű.

1.4.3. A gerjesztés módjai

Gerjesztés fénnyel

Ha a lézeranyag – amelyben tehát a populációinverzió megvalósul és ezáltal a fény indukált emisszió révén erősödik – szilárd fázisú, akkor a gerjesztési energiát általában fény formájában visszük be a közegbe. Az (1) lépés tehát a fény abszorpciója, amelynek során a foton teljes energiája átadódik az atomnak. A foton energiájának tehát pontosan meg kell egyeznie az (1) lépés felső és alsó energia szintjeinek különbségeivel. A gerjesztés akkor hatékony, ha a fotonok zöme megfelelő energiájú. Tehát például fehér fény esetén a felső nívónak nagyon szélesnek kell lennie. Ha a felső nívó keskeny, akkor viszont közel monokromatikus fényt kell gerjesztéshez használni.

Az első lézerekben a populáció inverziót még nem tudták folyamatosan fenntartani, a fényt villanólámpa (xenonlámpa) szolgáltatta. Folyamatos működésű (CW = continuous wave) lézereket természetesen folytonos fénnyel kell táplálni. Ez ma leginkább LED-del vagy egy másik lézerrel (félvezető lézerrel) lehetséges.

Geometriailag a lámpa csavarvonalszerűen is körbeveheti a lézeranyagot. Az első működő lézerben, amely rubinlézer volt (Maiman, 1960.), ez történt. Igen hatékony a fény átvitele a lámpából a lézeranyagba, ha ezek egy ellipszoid tükör (ellipszis alapú hasáb) egy-egy fókuszvonalán vannak. (Az ellipszoid tükör egyik fókuszpontjából induló fénysugarak mindegyike eljut a másik fókuszpontba.)

1.4.3.1. ábra: Rubinlézer gerjesztése csavarvonal alakú villanó lámpával

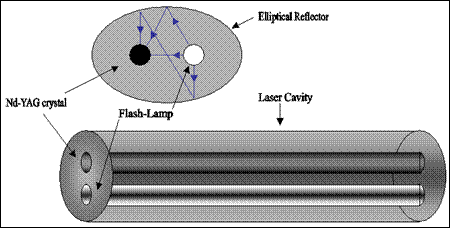
1.4.3.2. ábra: Nd:YAG lézer gerjesztése ellipszoid tükör geometriában

A fenti geometriákban a gerjesztő fényt a lézeranyagba a kialakuló lézersugárra merőlegesen vezetjük be. Hatékonyabb lehet a gerjesztés, ha a két fénysugár párhuzamos (vagy közel párhuzamos) egymással. Ezt a geometriát – mivel ez elválaszthatatlan a következő fejezetben ismertetendő tükörrezonátortól – itt még nem tudjuk részleteiben tárgyalni.

Gerjesztés elektromos kisüléssel (gázban)

Gőzfázisú lézeranyag esetén – és félvezető lézeranyag esetén is – a gerjesztési energiát közvetlenül elektromos árammal célszerű a lézeranyagba bevinni. Ezért a gázlézerek lényegében (a fénycsövekhez hasonló) kisülésű csövek. A kisülés lehet önfenntartó, amikor a töltéshordozók (elektronok és ionok) maguk is a kisülési folyamatokban keletkeznek. De lehetnek nem önfenntartók is, ekkor a töltéshordozókat valamilyen más mechanizmussal kell a lézeranyagban létrehozni.

Önfenntartó kisülés csak kis nyomású gázokban lehetséges. Ekkor a gáz annyira ritka, hogy az elektronok két ütközés között az ionizációs energiának megfelelő mozgási energiára tudnak gyorsulni. Az atommal ütköző elektron – a fotonnal ellentétben – nem veszik el az ütközés során, energiája egy részét megtartja. Az ionizációs energiát meghaladó energiájú elektronok – az energiájuktól függő mértékben ugyan, de képesek ionizációra is és/vagy gerjesztésre is. Az ionizáció során elektron keletkezik (ami a kisülés fenntartásához szükséges), a gerjesztés pedig a lézerműködés első lépése. Az önfenntartó kisülést általában a lézer tengelye irányába mutató elektromos térrel (axiális felépítés) valósítják meg.

Nagy nyomású gázban az elektronok szabad úthossza túl kicsi, ezért önálló kisülés bennük nem lehetséges. Ilyenkor a szabad töltéshordozókat más módszerrel (pl. ionizáció UV fénnyel, elektronágyú, stb.) kell bevinnünk. Ezekben a lézerekben az elektromos mező iránya általában merőleges a lézer tengelyére (transzverzális elrendezés). A sűrűbb gázban a fotonok természetesen gyorsabban tudnak szaporodni (egységnyi hosszra vonatkoztatva), ezért ezek a lézerek általában nagyobb teljesítményűek. Ezeket a lézereket TEA –lézereknek (Transzverzális Elektromos tér Atmoszférikus nyomás) is nevezik.

Megjegyezzük, hogy a félvezető lézerekben is a lézeranyagon átfolyó áram által bevitt energia tartja fenn a lézerműködést. Itt azonban a felső lézernívóra nem ütközés révén jutnak fel az elektronok.

1.4.3.3. ábra: Gerjesztés axiális (tengelyirányú) elektromos kisüléssel

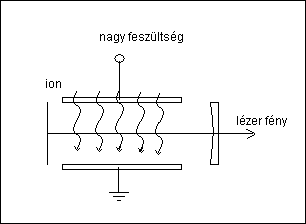
1.4.3.4. ábra: Gerjesztés transzverzális (keresztirányú) elektromos kisüléssel

1.4.4. A tükörrezonátor

Tételezzük fel, hogy az előző pontokban leírtak mindegyike teljesül. A megfelelő lézeranyagba megfelelő módon energiát pumpálunk és két meghatározott energiaszintre teljesül a populációinverzió feltétele. Ekkor a lézeranyagban elindult megfelelő frekvenciájú sugárzás exponenciálisan erősödik. Az első foton nyilvánvalóan csak spontán emisszióval keletkezhet, de a szaporodása indukált emisszióval történik. Mivel a lézerek tengelye mentén a sugárzás sokkal hosszabb utat tud a lézeranyagban megtenni, mint más irányokban, ezért az ilyen irányú sugárzás erősödik fel a legjobban. Ezt a hatást tovább fokozhatjuk, ha a tengelyre merőlegesen egy tükröt helyezünk el és a sugárzást a lézeranyagba visszajuttatjuk. Ezáltal a sugárzás sokkal hosszabb úton fog erősödni, végleg elnyomva minden más irányú sugárzást. Ha a lézeranyag másik oldalán is elhelyezünk egy tükröt – párhuzamosan az elsővel – akkor az oda-vissza verődések sorozatán keresztül a sugárzás tetszőleges szintig erősödhet. Valójában ez az erősödés nem tart a végtelenig – ahogy korábban is utaltunk rá – mert nagy intenzitásoknál az indukált emisszió lecsökkenti N₂-t. Ez a csökkenés határesetben N₁–ig tarthat, ekkor az indukált emisszió egyensúlyba kerül az abszorpcióval, a sugárzás nem erősödik tovább.

A két tükör egyikének természetesen félig áteresztőnek kell lennie, hogy a sugárzás egy részét kicsatolhassuk a lézerből, azaz lézersugarat nyerjünk. A másik tükörnek azonban lehetőleg 100 %-os reflexiójúnak kell lennie (zárótükör). Fontos hangsúlyozni, hogy a lézertechnika tükrei általában nem közönségesek, hanem a vékony réteg interferencián alapuló tükrök. Ezek csak az erősíteni kívánt egyetlen frekvenciát (és szűk környezetét) verik vissza – de azt 100 %-osan – a többit átengedik. Ezáltal a gerjesztő fény a tükrön keresztül is becsatolható a lézeranyagba, a lézer működéséhez nem szükséges fotonok viszont ugyanitt erősödés nélkül elhagyják azt.

Ismeretes, hogy a belső és visszavert hullámok interferenciája állóhullámot eredményez. Az állóhullámban a helyfüggés a fázisból az amplitúdóba tevődik át, ami maximális amplitúdójú (duzzadóhely) és zérus amplitúdójú (csomópont) helyeket eredményez a lézer tengelye mentén. Mivel a tükrök felületén mindenképpen csomópont van és két szomszédos csomópont távolsága λ/2, ezért a két tükör távolsága ennek egész számú többszöröse kell, hogy legyen. Ha a tükrök távolsága (azaz a tükör rezonátor L hossza) ettől eltér, akkor a sugárzás a rezonátorban nem erősödik. A valóságban inkább az a helyzet, hogy a tükör rezonátor a ráeső sugárzásokból a

(ahol n egész szám)

feltételnek megfelelő sugárzásokat szelektív módon felerősíti. Az ábrán egy tükörrezonátor sematikus rajza látható, a bal oldali a félig áteresztő tükör, azaz a kicsatoló tükör. Ebben a rezonátorban csak 18 db félhullám fér el.

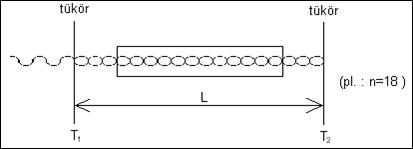
1.4.4.1. ábra: A tükörrezonátor sémája

A gyakorlatban n ennél általában sokkal nagyobb, például egy 0,3 m-es rezonátorban a 633 nm hullámhosszú vörös fényből kb. 948 ezer félhullám fér el.

A tükörrezonátor ettől a példaként adott hossztól sokkal rövidebb (pl. koronglézer) és sokkal hosszabb (pl. szállézer vagy fiberlézer) is lehet. Ez utóbbi lézerben a megfelelően adalékolt vékony üvegszál (vagy más anyag) a lézeranyag és egyben a tükörrezonátor is. A tükrök szerepét a szálvégek periodikus törésmutatójú tartománya játssza. Az üvegszálból a fény oldalt nem tud kilépni, a tükörrezonátor tehát föl is tekercselhető, ami jelentősen csökkentheti a lézer helyigényét.

A tükörrezonátort – különösen az elektromérnöki személet szerint – felfoghatjuk úgy is, hogy ez szolgáltatja az erősítő visszacsatolását. Ez a visszacsatolás a rezonanciafrekvenciákon pozitív, ilyekor az erősítő „begerjed”, más frekvenciákon a visszacsatolás negatív. A lézert általában pozitívan visszacsatolt rezgéskeltőként és nem külső, gyenge jelek erősítésére használjuk.

A tükörrezonátor a lézerműködésnek nem elengedhetetlen feltétele. Vannak olyan lézerek, amelyek nem tartalmazzák (pl. röntgen-lézer).

A tükörrezonátor hatása a lézerfény frekvenciájának a kiszélesedésére

A fenti képletben a hullámhosszat frekvenciára is átírhatjuk (f= c/λ), ekkor, ahol n egész szám. Kifejezve a frekvenciát f= n·c/(2L) azt kapjuk, hogy a rezonátor által erősített frekvenciák közötti távolság (azaz két szomszédos longitudinális módus frekvencia távolsága):

.

A fenti adatokkal ez a frekvencia távolság éppen 5·10⁸Hz. Tehát a tükörrezonátor egymástól 500 MHz távolságra lévő frekvenciákat fog erősíteni. Vegyük észre, hogy ez a frekvencia távolság ugyan kb. hat nagyságrenddel kisebb az optikai frekvenciáknál, de nagyobb a tipikus természetes vonalszélességnél. Véletlenszerűen választott rezonátorhossz esetén tehát előfordulhat az, hogy az erősíteni kívánt frekvencia éppen két módus közé esik, és a lézer az adott rezonátorhosszal nem működik.

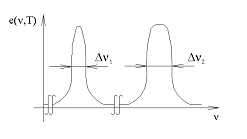
A valóságban azonban ez ritkán fordul elő, mert a spektrumvonalak sokkal szélesebbek a természetes vonalszélességnél. Ennek az oka pedig az atomok hőmozgása miatti Doppler- kiszélesedés. Ha az atom haladási irányában bocsátja ki a fotont, akkor a nyugvó megfigyelő a foton frekvenciáját nagyobbnak, ellenkező esetben pedig kisebbnek érzékeli. A relatív frekvenciaváltozás közelítőleg v/c, ami szobahőmérsékleten közepes tömegű atomokra átlagosan kb. 10^-6 körül lehet. Azaz a Doppler-effektus már szobahőmérsékleten is a módus távolsággal egyezőre (vagy azzal nagyobbra) szélesíti a lézernívót. Ezen a szélesebb frekvenciatartományon a tükörrezonátor egy vagy néhány frekvenciát erősíteni fog, ezek lesznek a lézer longitudinális (hosszirányú) módusai. Egy-egy módus szélessége sokkal kisebb is lehet a természetes vonalszélességnél.

Az ábrán látható spektrumú lézer 5 darab megengedett frekvenciával, azaz 5 db longitudinális módussal rendelkezik. Ezek a módusok nemcsak frekvenciában különböznek, de a fázisaik is függetlenek egymástól. Bizonyos alkalmazásokat (pl. interferencia kísérleteket) ez a tény lehetetlenné tenne, ezekben csak egyetlen longitudinális módus maradhat. Az oldalmódusok elnyomására különböző módszerek ismertek. Használhatunk például interferométert, amely csak az egyik módust engedi át. Másik lehetőség a rövid rezonátor alkalmazása, amellyel a szomszédos módusok olyan távolra kerülhetnek, hogy az erősítési görbe alá közülük csak egy darab fér be.

természetes vonalszélesség

Df_nat »10⁷ Hz

A Doppler-effektus hatására ez kiszélesedik

Df_Doppler »10⁹ Hz

a longitudinális lézermódusok frekvencia távolsága

Df_long »10⁸ Hz

egy módus kiszélesedése tipikusan

Df_lézer »10⁶ Hz

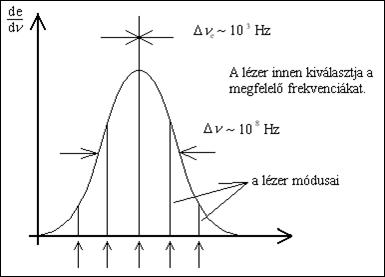
megfelelnek az feltételnek

1.4.4.2. ábra: Lehetséges frekvenciák a tükörrezonátorban

A képlet alapján kiszámíthatjuk a fenti frekvencia kiszélesedéseknek megfelelő koherenciahosszakat is. Ezek szerint a természetes vonalszélességnek megfelelő 3m-es koherenciahosszat a hőmozgás miatti Doppler-kiszélesedés 3 cm-re rontja, viszont a tükörrezonátor (ha csak egyetlen transzverzális módus van) 30m-re javítja.

A tükör rezonátorban a fentebb ismertetett, kettő darab párhuzamosan elhelyezett síktükör helyett gyakran használnak homorú tükröt (tükröket) is. Ezek beállítása könnyebb, stabilabbak, de nagyobb divergenciájú lézernyalábot eredményezhetnek. Stabil lézernyalábot csak bizonyos elrendezésekben kaphatunk, pl:

a) 2 db homorú tükör konfokális elrendezésben (közös a fókuszuk),

b) 2 db homorú tükör koncentrikus elrendezésben (közös a görbületi középpont),

c) félgömbi elrendezés (a homorú tükör fókusza a síktükörre esik).

A tükörrezonátorban – függően a tükrök alakjától és méretétől - különféle állóhullám módusok alakulhatnak ki. Ezeket keresztirányú (transzverzális) módusoknak (TEM = Transversal Electromagnetic Mode) nevezzük. A transzverzális módusok leginkább a lézernyaláb keresztirányú intenzitás eloszlásában mutatkoznak meg. A legfontosabb módus az alapmódus (TEM₀₀) amely egyetlen maximummal rendelkezik és eloszlása a Gauss-függvénnyel jellemezhető:

,

a transzverzális alapmódust ezért Gauss-nyalábnak is nevezik. Ez a módus eredményezi a legkisebb divergenciájú, legjobban fókuszálható nyalábot, sok alkalmazásban más módusa nem is lehet a lézernek.

Vannak azonban más transzverzális módusok is, különösen vastag, nagy teljesítményű lézereknél. Ezeknek keresztirányban több maximumuk van, metszete foltokból, esetleg kör(ök)ből áll, ami nagyobb nyalábdivergenciát eredményezhet. Az 1.4.4.3. ábra néhány keresztirányú módust szemléltet a hozzá tartozó jelölésrendszerrel és az általuk létrehozott energia-eloszlással.

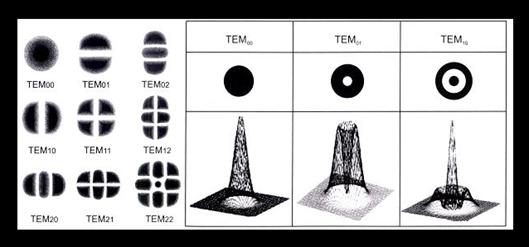
1.4.4.3. ábra: A lehetséges transzverzális módusok két különböző geometriában

A TEM-nél megkülönböztethető polár koordinátarendszerben felvett teljesítmény-eloszlás (TEM_pl), illetve derékszögű koordináta rendszer szerinti (TEM_nm). Attól függően, hogy milyen a berendezés felépítése, optikai rendszere, a hozzá jobban illeszekedő módus-szerkezetet adják meg. Az indexben szereplő számok a tengelyek mentén a lokális intenzitás minimumok számát jelentik, a végtelenben lévő 0 értéket nem számítva. A TEM₀₀, mindkét rendszerben az ideális Gauss eloszlást jelenti. A TEM indexek megadása mellett a kevert módusokat a sugárminőség és a sugárparaméter jellemzi.

Ha több módus is lehetséges, azok a legtöbb esetben egyszerre vannak jelen a rezonátorban, természetesen – hasonlóan a longitudinális módusokhoz - egymástól független fázissal. Az interferenciás kísérletek tehát nemcsak azt követelik meg, hogy a lézernyaláb egyetlen longitudinális módusból álljon, hanem azt is, hogy transzverzális alapmódusú legyen.

1.5. A fontosabb lézertípusok konkrét konstrukciói, működésük és jellemzőik

1.5.1. Gázlézerek: a He-Ne és a CO₂ lézer

He-Ne lézer

A hélium-neon lézer egy néhány mm vastag és néhány dm hosszú kisülési cső, amelyben kisnyomású (néhány mbar) hélium-neon gázkeverék van, amelyben a hélium és neon aránya tipikusan 7:1. Az elektródák a kisülési cső két végén (vagy annak közelében) vannak elhelyezve, így az elektromos mező axiális. Az elektromos kisülésben az elektronokkal történő ütközések során a gázatomok gerjesztődnek és ionizálódnak. A legfontosabb gerjesztés a többségben lévő hélium atomoknak az alapállapotból (1s²) az első gerjesztett állapotba (1s2s) történő gerjesztése, amelyhez meglehetősen nagy energia szükséges (~20,5 eV). A kialakult gerjesztett állapot metastabil, mert visszafelé az emissziós folyamattal történő átmenet tiltott. Ebben a gerjesztett állapotban tehát a hélium atomok nagyon felszaporodnak. A neonatomnak azonban van egy pontosan ilyen energiájú gerjesztett állapota (2p⁵5s), amelynek ez a gerjesztési energia ütközéssel átadható. Ezt az ütközési folyamatot szokás másodfajú ütközésnek is nevezni:

He* + Ne → He + Ne* (a * jel a gerjesztettséget jelenti)

A héliumatomok tehát másodfajú ütközéssel jutnak vissza az alapállapotba, a 20,5 eV-es gerjesztési energiák pedig (szinte kivétel nélkül) a neon atomokhoz jutnak. A neon atomok pedig nem adják vissza, mert a 2p⁵5s állapotuk viszonylag gyorsan elbomlik.

Fontos hangsúlyozni, hogy a másodfajú ütközés következtében a neonatomok úgy tudnak a 2p⁵5s gerjesztett állapotba kerülni, hogy az alacsonyabb energiájú gerjesztett állapotokat kihagyják. Elvben ugyan a neon 2p⁵5s gerjesztése közvetlenül elektronütközéssel is bekövetkezhet (és ekkor az alsóbb állapotok is gerjednek), de ez a neon kis aránya miatt kisebb valószínűségű.

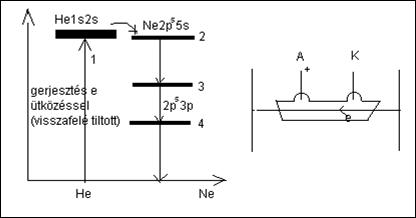
1.5.1.1. ábra: A He-Ne lézer energiaszintjei

A populációinverzió tehát, a kisebbségben lévő neonatomok két olyan magasan gerjesztett állapota között valósulhat meg, ahol az alsó nívó rövidebb élettartamú. A mai He-Ne lézerekben a 2p⁵5s állapot jelenti a felső lézernívót, a 2p⁵3p pedig az alsót, a közöttük történő átmenet során a lézer 633 nm hullámhosszúságú vöröses színű fényt bocsájt ki. Mint említettük, az alsó lézernívó (a 2p⁵3p állapoton keresztül) gyorsan kiürül. Az elmondottakból következik, hogy a He-Ne lézer négyszintű (alapállapot, He(1s2s), Ne(2p⁵5s), Ne(2p⁵3p)) és folytonos üzemű.

Ennek a lézer típusnak a hátránya, hogy nagyon magasan van a He 1s2s gerjesztett állapota (20,5 eV), a lézer foton energiája ennél éppen egy nagyságrenddel kisebb (~2,0 eV). Ez a tény eleve 10% alá viszi a hatásfokot. Számos itt nem részletezett atomfizikai folyamat ennek a töredékére csökkenti az elvi hatásfokot, a gyakorlati hatásfok pedig az 1%-ot sem éri el. A He-Ne lézerek általában csak néhány mW teljesítményűek.

A nemesgáz töltés nagy előnye, hogy az a lézerműködés során nem használódik el, nem keletkeznek a lézerműködést károsan befolyásoló a lézerből eltávolítandó vegyületek

Ha a rezonátor tükreit a kisülési csövön kívül helyezzük el, akkor célszerű a cső végeit Brewster szögben levágni. Ekkor a fény sokszoros áthaladás után a beesési síkban polárossá válik. Ezáltal a lézer működése stabilabb lesz, továbbá számos esetben a lineárisan poláros lézerfény alkalmazása is kedvezőbb.

A CO₂ lézer

A molekuláris lézerekben a gerjesztés nem az atomi héjakon, hanem az ennél sokkal kisebb molekuláris energiaszinteken történik. Ezek az energiaszintek a molekulák forgásából (rotációs energiaszintek) és rezgéséből (vibrációs energiaszintek) származnak. A vibrációs szintek tipikusan néhány tized eV-nyi energiával gerjeszthetők, a rotációs szintek ennek századával. A rotációs szintek tehát igen közel vannak egymáshoz, ezeket az energiákat gyakran folytonosnak tekintjük és sávos energiaszerkezetről beszélünk. A hőmozgás energiája szobahőmérsékleten sokkal nagyobb a rotációs szintek különbségénél, de kisebb, mint a vibrációs szintek energiája. Tehát mondhatjuk, hogy szobahőmérsékleten a molekulák forognak, de még nem (vagy alig) rezegnek.

A szén-dioxid molekula háromféle rezgési módusban rezeghet. A legkisebb energiájú (~ 0,1 eV) a torziós rezgés, amikor az atomok a molekula tengelyére merőlegesen rezegnek, periodikusan v betűt formázva. Ennél nagyobb energiájú (~ 0,2 eV) a molekulatengely irányába eső szimmetrikus rezgés, amelyben a két szélső oxigénatom rezeg, de a középen lévő szénatom nyugalomban van. A legnagyobb energiájú (~ 0,3 eV) rezgési módus az aszimmetrikus rezgés, amelyben a középső szénatom rezeg a molekulatengely mentén. (Ilyenkor persze az oxigén atomok ellenütemben mozognak, hogy a tömegközéppont nyugalomban legyen.)

A lézer rezonátorába adagolt nitrogéngáz (N₂) a CO₂ molekulák aszimmetrikus rezgési szintre való szelektív gerjesztését eredményezi. Ez a folyamat nagyban hasonlít a hélium-neon lézernél leírt másodfajú ütközéshez.

A lézerműködés az aszimmetrikus és szimmetrikus rezgési módusok bizonyos forgási szintjei között jön létre. A kibocsájtott sugárzás hullámhossza – a kb. 0,1 eV energiakülönbségnek megfelelően – 10,6 µm, amely a távoli infravörös tartományba esik. A N₂ – CO₂ keverékhez adagolt segédgázok (pl. hélium, vízgőz) segítik az alsó lézernívó kiürülését és hűtik a gázkeveréket.

	Aszimmetrikus rezgés
	Szimmetrikus rezgés
	Torziós rezgés

1.5.1.2. ábra: A CO₂ molekula lehetséges rezgései

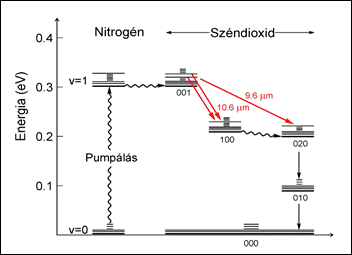
1.5.1.3. ábra: A CO₂ lézer energiaszintjei

Az elmondottakból következik, hogy a CO₂ lézer is négyszintű (alapállapot, N₂(vibr), CO₂ (aszimm.), CO₂ (szimm.)) és képes a folytonos üzemre.

A széndioxid lézer nagy hatásfokú, mert a gerjesztés igen kis energiát igényel és ennek az energiának a nagy része átadódik a lézernyalábra. A lézernyaláb teljesítménye igen nagy is lehet (~10 kW), különösen a nagy nyomású verziókban (TEA lézerek). A hatalmas teljesítmény intenzív vízhűtést tesz szükségessé, hogy a lézerközeg hőmérséklete a szobahőmérséklet közelében maradjon. A molekulák a gázkisülésben széteshetnek, más molekulákká egyesülhetnek, amelyek gátolhatják a lézerműködést. Ezért CO₂ lézerben – hasonlóan a többi molekuláris lézerhez – gondoskodni kell a friss gáz folyamatos be- és az elhasznált gáz folyamatos kiáramoltatásáról.

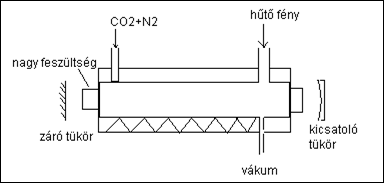
1.5.1.4. ábra: A CO₂ TEA lézer vázlata

1.5.2. Ionlézerek: az argon-ion lézer.

Az ionlézerekben a lézernívókat a gerjesztett ionállapotok jelentik. Az egyes állapotok elektronütközéssel történő gerjesztésének hatékonysága igen eltérő lehet, és nagyon eltérő lehet az állapotok élettartama is. Ezek következtében könnyen előfordulhat, hogy egy nagyobb energiájú gerjesztett ionállapotban feldúsul az ionok száma, míg valamelyik alatta lévő szinten lecsökken. A legtöbb ionfajta esetében találhatunk ilyen populációinverzióra hajlamos energiaszint kettőst.

Az ionlézerek talán legfontosabb képviselője az argon-ion lézer. Mint tudjuk az argon alapállapoti elektronkonfigurációja 3p⁶, az argon-ioné 3p⁵, a legfontosabb gerjesztett argon-ionoké pedig 3p⁴4s és 3p⁴4p. Ezek a szintek valójában – a 3p és a 4s vagy 4p elektronok perdületeinek különböző kapcsolódásai miatt – sok egymáshoz közeli szintet jelentenek. A 3p⁴4p állapotok populációja – atomfizikai okok miatt – általában nagyobb mint a 3p⁴4s állapotoké, így köztük folyamatosan populációinverzió áll fenn.

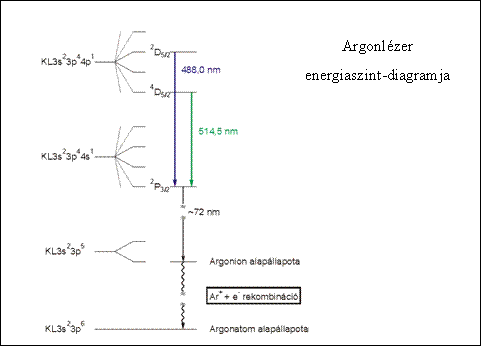
1.5.2.1. ábra: Az argon-ion lézer energiaszintjei

Az argon-ion lézer nagyobb teljesítménnyel a 488 nm-es (kék) és az 514,5 nm-es (zöld) hullámhosszakon tud működni. Vannak más, kisebb teljesítményű hullámhosszai is (pl. 457,9 nm (ibolya)). Ezek külön-külön és együttesen is működhetnek, ez utóbbi esetben az argon-ion lézer fénye kékesfehér. Az elmondottakból következik, hogy ez a lézer négyszintű (3p⁶, 3p⁵, 3p⁴4s és 3p⁴4p) és folytonos üzemű.

Az argon-ion lézer működéséhez arra is szükség van, hogy a gerjesztett ionállapotok nagy koncentrációban legyenek jelen. Ezt nagy gerjesztő áramsűrűséggel lehet elérni, ami az argont erősen ionizált, magas hőmérsékletű plazma állapotba juttatja. A magas hőmérséklettől a lézercső falát a plazma mágneses térrel történő koncentrációjával lehet valamelyest védeni. A fal ennek ellenére is nagyon felmelegszik, ezért különleges anyagból kell készíteni és erősen kell hűteni.

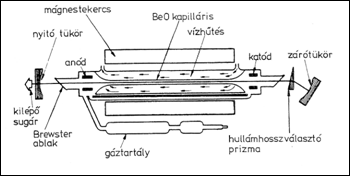
1.5.2.2. ábra: Az argon-ion lézer felépítése

1.5.3. Szilárdtest lézerek: a rubinlézer, a Nd-YAG-lézer.

Rubinlézer

Az első működő lézer a rubinlézer volt, amelyet Maiman 1960-ban épített meg. A lézerközeg egy kb. 10 cm hosszú hengeres alakú szintetikus rubinkristály volt. A tükörrezonátort a henger simára és párhuzamosra csiszolt alakjai jelentették. A kristályt xenon villanólámpával gerjesztették, amely csavarvonalszerűen körbevette azt.

Mint tudjuk a rubin krómionokkal szennyezett alumínium-oxid (Al₂O₃). Ez a kristály a fehér fény kék-zöld részét nagyon erősen abszorbeálja. A gerjesztés után az elektronok egy széles energiasávba jutnak. Ebből a sávból az elektronok foton kibocsájtásával visszahullhatnak az alapállapotba is, de a többségük egy sugárzásmentes folyamattal közbenső metastabil energiaszintekre kerül. (Sugárzásmentes folyamatban a felszabadult energia a kristályrácsot alkotó atomok rezgési energiáját növeli.) Igen intenzív fényforrással elérhető az, hogy az eredetileg alapállapotú elektronok több mint 50 %-át átpumpáljuk a metastabil állapotokba. Így populációinverzió alakulhat ki (legalábbis egy pillanatra) a metastabil állapotok és az alapállapot között. Az alsó és felső lézernívót tehát ezek az állapotok jelentik. A köztük tartozó átmenethez tartozó fénynek, a rubinlézer mélyvörös fényének a hullámhossza 694,3 nm.

A fentiek alapján a rubinlézer háromszintű (alapállapot, abszorbciós sáv, metastabil állapot), amelyben a folyamatos populációinverziót nehéz megvalósítani. A rubinlézer hatásfoka kicsi, ennek ellenére a teljesítménye egészen nagy is (néhányszor tíz watt) lehet. Ez csak igen nagy teljesítmény betáplálásával lehet elérni, ami viszont folytonos üzemben nem oldható meg. A rubinlézerek tehát impulzus üzeműek.

1.5.3.1. ábra: A rubinlézer energiaszintjei

A Nd:YAG lézer

A rubinlézer legnagyobb hátránya az, hogy háromszintű. Négyszintű lézert úgy nyerhetünk, ha a szennyező króm ionokat neodímium (Nd) ionokra cseréljük, az alumíniumoxid mátrixot pedig üvegre vagy yttrium-alumínium-gránátra (YAG) cseréljük. Ez utóbbi azért kedvezőbb, mert a gránátnak nagyobb a hővezető képessége, ezért jobban hűthető. Az így kapott lézer, amelyet Nd:YAG lézernek nevezünk, talán a legfontosabb szilárdtest lézer, akár hatalmas (~kW) teljesítményre is képes. Az ábra a YAG anyagba ágyazott Nd³⁺ ionok energianívóit mutatja.

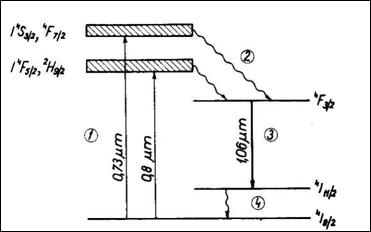
1.5.3.2. ábra: A Nd:YAG lézer energiaszintjei

Az (1) gerjesztés a látható és infravörös határán lévő fénnyel történik, amely legtöbb esetben LED-ből, illetve félvezető lézerből származik. (A kiindulásként alkalmazott lézerfény tulajdonságai igen gyengék a végeredményként kapott lézerfényhez képest.) A (2) folyamat itt is sugárzásmentes átmenetet jelent. A (3) lézerátmenet során kapott infravörös lézerfény 1064 nm hullámhosszúságú. Az alsó lézernívó kiürülése (4) szintén sugárzásmentes.

Ezt a lézerfényt egy nemlineáris optikai anyaggal frekvencia kettőzéssel (azaz hullámhossz felezéssel) könnyen a láthatóba transzformálhatjuk (λ/2 = 532 nm, zöld).

1.5.4. A félvezető lézerek.

A leggyakrabban használt lézertípus a félvezető lézer, amelyet gyakran lézerdiódának is nevezünk. Egyszerűbb változata egy „n” típusú és egy „p” típusú félvezető rétegből áll. (Az „n” típusú félvezetőben a legfelső energiasávban (a vezetési sávban) lévő elektronok, a „p” típusú félvezetőben az alatta lévő sávban (a vegyérték sávban) lévő elektron hiányok (lyukak) vezetik az elektromosságot.) A lézersugár e két réteg közötti néhány mikrométer vastag határrétegben alakul ki. Nyitóirányú áram hatására a határrétegbe az „n” típusú rétegből elektronok a „p” típusú rétegből lyukak áramlanak be. Amikor az elektronok a lyukakba „esnek” a felszabaduló energiát egy foton viszi el. Ez utóbbi azonban csak néhány különleges félvezetőben (a direkt félvezetőkben, pl. GaAs) történik meg. A félvezetők többségében a felszabadult energiát a foton nem tudja elvinni, mivel ahhoz nagy lendület is társul. Ezekben a félvezetőkben a felszabadult energia rácsrezgéssé alakul, azaz melegíti a határréteget.

Az alkalmas félvezető (pl. GaAs) határrétegében egyesülő lyukak és elektronok tehát fény bocsájtanak ki. Ez a fény azonban indukált emisszió révén csak akkor erősödik, ha populációinverzió áll fenn, azaz a felsősáv alján több elektron tartózkodik, mint az alsó tetején. Ez csak nagy áramsűrűségeknél teljesül, kisebb áramsűrűségeknél nincs inverzió és a fény erősödés nélkül kijön a határrétegből (LED).

A hatékony erősítéshez tükörrezonátor is kell, ebben a lézertípusban a tükröket a félvezető kristály szigorúan párhuzamosra polírozott véglapjai jelentik. Adott áramsűrűség fölött tehát beindul a lézerműködés, ekkor a széles spektrum és irányeloszlás hirtelen „összeugrik”.

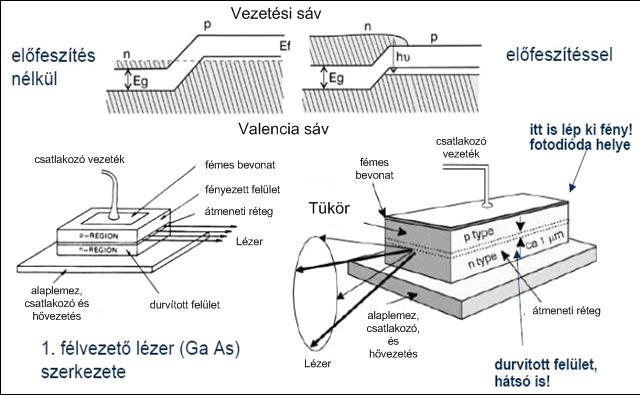
1.5.4.1. ábra: A félvezető lézer energiaszintjei és felépítése

Az első félvezető lézerek magas áramküszöbűek voltak, csak lehűtve és csak infravörös tartományban működtek. Az újabb ún. heteroátmenetes félvezető lézerek már igen kedvező tulajdonságúak. Ezekben például a „p” és „n” típusú GaAs rétegek között olyan rétegek is vannak, amelyekben a Ga atomok egy részét Al atomokra cserélték (Ga_1-xAl_xAs). A széles körben használt lézerpointerek is félvezető lézerek, ezek fénye kb. 650 nm-es hullámhosszú és vörös színű.

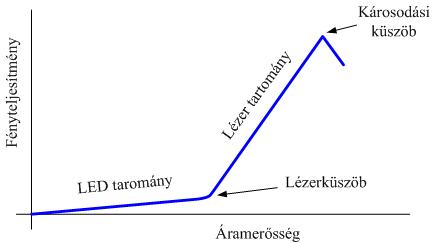
1.5.4.1. ábra: A LED/félvezető lézer karakterisztikája

1.6. A lézerfény legfontosabb tulajdonságai

Mint korábban is említettük, a lézerfény lehet folytonos (CW), de lehet impulzus üzemű is. Ez utóbbi esetben a lézerimpulzus hosszát és ismétlődési frekvenciáját is ismernünk kell. A lézersugár – a lézer belső felépítésének megfelelően – lehet polarizált (poláros) és polarizálatlan is. Az alkalmazások jelentős része poláros lézernyalábot követel meg.

A lézersugár további tulajdonságai – irányítottság, monokromatikusság és teljesítmény – tekintetében igen különleges, ami más fényforrások által elérhetetlen.

Általánosságban elmondhatjuk, hogy az irányítottság és monokromatikusság akkor a legkedvezőbb, ha a lézer longitudinális és transzverzális alapmódusban működik. Ezt a nem kívánatos módusok elnyomásával tudjuk elérni, tehát a teljesítmény ilyenkor nem túl nagy. A nagy teljesítményű lézernyalábok általában sok longitudinális és transzverzális módust tartalmaznak.

Az irányítottságot a lézernyaláb divergenciájával jellemezzük. Ennek minimális mértéke elméletileg , amint azt egy korábbi fejezetben levezettük. Ezt az elvi határt csak a transzverzális alapmódusú (TEM₀₀) lézerek tudják megközelíteni. A divergencia függvénye a lézernyaláb átmérőjének, nyalábtágítással tehát csökkenthető. Kis divergenciájú nyalábok kisebb foltra fókuszálhatók. Első közelítésben a folt átmérője (D) a lencse fókusztávolságának (f) és a nyalábdivergenciának a szorzata:

Ennek legkisebb értéke (ha f ~ πd) a hullámhossz körüli érték.

A monokromatikusságot a lézerfény frekvencia kiszélesedésével jellemezhetjük, ez – egyetlen longitudinális módus esetén – sokkal kisebb lehet a természetes vonalszélességnél is. A keskeny spektrumvonalhoz – amint az egy korábbi fejezetben láttuk – nagy koherenciahossz tartozik. A nagy koherenciahossznak különösen az interferenciás mérésekben van jelentősége. A kis divergencia és kis frekvencia kiszélesedés leginkább a gázlézerek lézerfényét jellemzi, a félvezető lézerek ebben a tekintetben nem kiemelkedőek.

Ha a lézerek teljesítményéről beszélünk, akkor élesen meg kell különböztetnünk a folytonos üzemű lézerek teljesítményét és az inpulzusüzemű lézerek csúcsteljesítményét. A folytonos üzemű lézerek közül a kisnyomású gázlézerek (pl. He-Ne) teljesítménye gyakran a mW-ot sem éri el, a nagynyomású CO₂ lézerek és a Nd: YAG lézerek folytonos teljesítménye 10 kW is lehet. Az inpulzusüzemű lézerek csúcsteljesítménye erősen függ az impulzusidők hosszától. Nyilvánvaló, hogy adott átlagteljesítmény mellett a csúcsteljesítmény akkor nagyobb, ha az impulzusidő rövidebb. Egy ps (= 10^-12 s) impulzusidő esetén a csúcsteljesítmény akár a 10¹⁴ W-ot is elérheti.

A nagy teljesítmény és jól fókuszálhatóság együttesen a fókuszált lézernyalábban különösen nagy teljesítménysűrűséget jelent. Ha például egy 1 kW-os lézernyalábot egy 10 µm²-es foltra fókuszálunk, akkor az 10¹⁴ W/m² teljesítménysűrűséget jelent, amely a Nap felszínén mérhető értéket hat nagyságrenddel meghaladja. Ha pedig a spektrális teljesítménysűrűséget tekintjük, akkor azt is figyelembe kell vennünk, hogy ezt a teljesítményt a lézer keskeny frekvenciatartományban sugározza ki (pl. Df_lézer »10⁸ Hz). Ha ezt a Nap sugárzásának 10¹⁴ Hz széles spektrumához viszonyítjuk, akkor a lézer a Napot egybilliószorosan (10¹²) is felülmúlhatja.

1.7. Precíziós lézerinterferometrikus elmozdulásmérés

A precíziós lézerinterferometrikus elmozdulásmérő lényegében egy Michelson interferométer, amelyben a polarizáció felhasználásával a pontosságot megnöveltük és a mozgás irányát is mérhetővé tettük. A megnövelt pontosság λ/8.

Felépítése:

1, Lézer:

- He-Ne lézer (λ=632,8 nm)

- belső tükrös

- rögzített polarizációs irány (Brewster ablak)

- hossza kb. 12 cm

- teljesítmény: P~3 mW (3A biztonsági osztály)

- nyalábdivergencia: ν~10 mrad

- longitudinális módustávolság: 1070 MHz

- sávszélesség: kb. 1500 MHz (rezonátor nélkül)

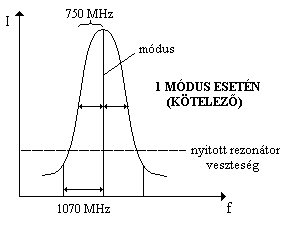
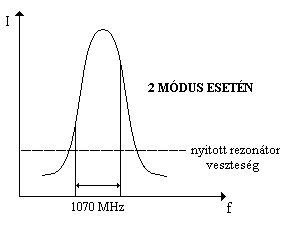
Ez a lézer egy vagy két longitudinális módusban tud működni. Az interferométerhez viszont kötelező az egy long. módusú működés. Ha egy módust pontosan az erősítési görbe közepére állítunk, akkor ez lesz az egyetlen módus. Ugyanis a szomszédos (1070 MHz-ra lévő) módusok a veszteségi szint alá szorulnak és elhalnak (bal oldali ábra). Ha a lézer elhangolódik (a módus nem pontosan az erősítési görbe közepén van), akkor feléledhet az egyik oldalsó módus is (jobb oldali ábra), tekintve, hogy az erősítési görbe sávszélessége nagyobb, mint a módustávolság. Az elhangolódást a rezonátor hosszának a változása okozza, ami a hőtágulás következmény lehet. A biztonságosan egymódusú működéshez (TEM₀₀ módus (Gauss nyaláb)) tehát a rezonátorhosszat néhány század fokra stabilizálni kell (Ha ΔT=1^oC, akkor Δl~0,5 μm => Δl stabil kb. 0,2 μm-re)

2, Nyalábtágító: Ez lényegében egy fordított Kepler-távcső. Ha megértjük a Kepler-tavcső működését, megértjük a nyalábtágítóét is.

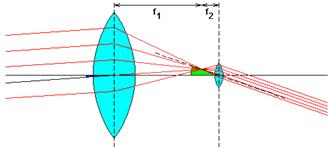
A távcső a (kvázi)végtelenben lévő tárgyat a végtelenbe képezi le. A párhuzamos fénysugarak a leképezés után is párhuzamosak, de az optikai tengellyel bezárt szögük megnövekszik az f₁/f₂ aránynak megfelelően (mintha közelebb mentünk volna). A távcső látószöget nagyítása természetesen a beérkező nyaláb divergenciájára is vonatkozik Mindeközben (az ábrán is látható módon) a távcsőbe érkező fénynyaláb be is szűkül a fókusztávolságok arányának megfelelően. (A tényleges távcsövek esetén ez a pupilla méretéig célszerű.) A távcső tehát a látószöget és a nyalábdivergenciát növeli, a nyalábátmérőt viszont csökkenti (nyalábszűkítő).

Ha a távcsövet megfordítjuk, akkor mindez ellentétessé válik. A fordított távcső tehát a látószöget és a nyalábdivergenciát csökkenti, a nyalábátmérőt viszont növeli (nyalábtágító).

Miért kell a lézernyalábot tágítani?

• Mert a tágabb nyalábok átfedése (legalábbis középen) jobban biztosítható
• Mert a lézernyaláb még párhuzamosabb lesz, ami nagyobb útkülönbségek esetén is lehetővé teszi az interferenciát.

3, Polarizációs nyalábosztó prizma (PNy)

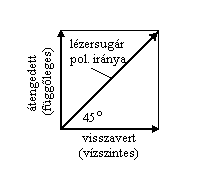
A nyalábosztó egy olyan eszköz, ami a beeső nyalábot két kb. egyforma intenzitású, egymásra merőlegesen továbbhaladó nyalábra osztja. Ez a jelen esetben prizma alakú, ill. egész pontosan két egyenlőszárú derékszögű háromszög alapú hasáb, amit egy kockává illesztettünk össze. A két hasáb közötti határfelület osztja ketté a nyalábot. A nyalábosztó prizma azért polarizációs, mert visszavert és átengedett lézersugár polarizációs iránya egymásra merőleges. A lézerfény eredetileg a függőlegessel 45^o-os szöget bezáró pol. iránnyal rendelkezik. Az ábrán az áthaladás után a hullám függőlegesen polarizált, a visszavert pedig vízszintesen.

4, Sarokprizma: A sarokprizma három egymásra merőleges tükröző felülettel ellátott háromszög alapú gúla (lényegében egy üvegkocka lapátlók mentén levágott csúcsa). Az alapon keresztül a prizmába bejutó fénysugár a három oldallapon történő egy-egy teljes visszaverődés után a prizmából az eredeti fénysugárral párhuzamosan lép ki. (Tulajdonképpen a járművek lámpáinak a macskaszeme is ilyenekből áll.) Az ábrán a sarokprizma egyszerűsített kétdimenziós modellje látható.

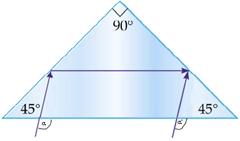
A sarokprizma előnyei a „sima” tükörhöz képest:

- 100% reflexió (teljes visszaverődés)

- a párhuzamosság mindig biztosított (nincs szögi hiba)

- a nyalábot eltolja, ezáltal szétválik a beeső és a visszavert nyaláb.

5, Polarizációs nyalábosztó prizma (ujra): A nyalábosztáskor a PNy-n szétválasztott hullámkomponensek (fénysugarak) a sarokprizmákról visszaérkeznek a PNy-ra. Mindkét visszaérkező fénysugár megtartja a polarizációs irányát. Tehát a PNy-n áthaladt fénysugár most is áthalad (100%-ban), a visszavert fénysugár most is visszaverődik (100%-ban). Tehát végeredményben mindkét sugár (az ábrán) vízszintesen lép ki a prizmából, a kétféle úton érkező hullám egyesül.

Tudjuk azonban, hogy az egymásra merőleges polarizációjú hullámok nem interferálnak. Hogy lesz akkor itt interferencia? A válasz: Majd kell bele egy polarizátor!!!

A mérőegység kinagyítva:

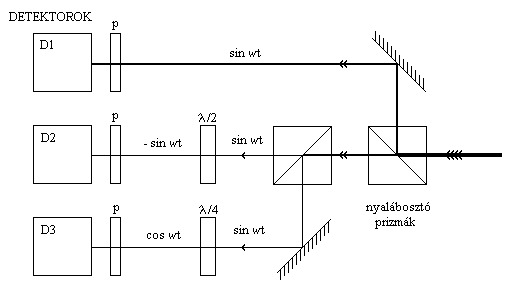
A λ/2 és λ/4 jelű eszközök fázistoló lemezek, amelyek a beeső fénysugár kétféle polarizációjú sugarának fázisát egymáshoz képest 2π/2= π-vel ill. 2π/4= π/2-vel eltolják. (A fázistoló lemezek működése a kettős törésen alapul, itt nem részletezzük.)

A p jelű eszközök polarizátorok.

Hogy áll a polarizátor?

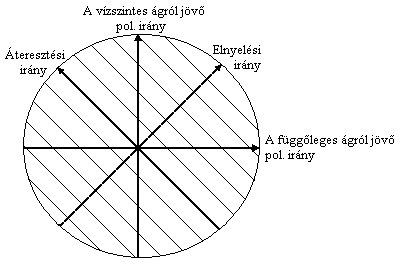
Mindkét polarizációs irány 45^o-ban álló komponensei interferálnak egymással.

Pl. tételezzük fel, hogy a két ágról érkező fénysugárban a térerősségek az ábrán jelzettek (tehát a +x és +y irányokba mutatnak. Ezek szuperpozíciója a polarizátor elnyelési irányába mutató térerősséget ad, azaz az interferencia végeredményben kioltást eredményez. Ha a fénysugarak áthaladnak a λ/2 lemezen, akkor az egyik térerősség irány ellentétesbe fordul. Így a térerősségek szuperpozíciója már a polarizátor áteresztési irányába mutató térerősséget ad, azaz az interferencia erősítést eredményez. Tehát a λ/2 lemez végeredményben (és a polarizátor segítségével) ellentétesbe fordítja az interferencia jellegét.

Még szemléletesebb, ha a saroktükör egyenletes mozgását tekintjük.

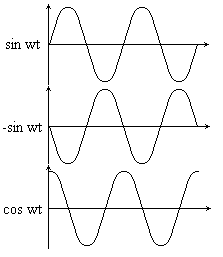
Ekkor az interferencia következtében a fényintenzitás periodikusan változik, pl. a szinuszfüggvény szerint.

A λ/2 lemez ezt a függvény mindenképpen az ellentétesbe fordítja, azaz a függvényt egy fél hullámmal eltolja.

A λ/4 lemez csak fele eltolást csinál, azaz koszinusz függvényt. Vagy mínusz koszinuszt, függően a tükör mozgási irányától.

A három grafikont egyben tekintve láthatjuk, hogy a maximumok ill. minimumok (ezeket tudják a fotodetektorok detektálni) λ/4 távolságra vannak. Az elmozdulás mérési pontossága – mivel oda-vissza út van – ennek a kétszerese, tehát λ/8. A He-Ne lézer esetében λ/8=632,8/8 nm= 79,1 nm. Ez kisebb, mint 0,1 μm, tehát az elmozdulás ilyen egységekben kijelezhető.

Ahogy fentebb is említettük, a három jel sorrendjéből következtethetünk a vízszintes ágban lévő sarokprizma mozgási irányára is.

Hangsúlyozzuk, hogy az elmozdulás mérési pontossága közel egy nagyságrenddel meghaladja az alkalmazott fény hullámhosszát, tehát lényegesen meghaladja a mikroszkópok felbontásának elvi határát is.

Szokás ezt a módszert szubmikronos elmozdulás mérésnek is nevezni.

Összefoglalva

- mindig a távolság változását, azaz az elmozdulást detektáljuk.

(egészen pontosan a nyalábirányú távolság változik)

(ha nem nyalábirányban mozog a rendszer => koszinuszos hiba)

- a mérés pontossága λ/8 ~ 0,08 μm

- túlságosan gyors mozgásokat nem képes követni (max. 150 mm/s-os sebesség)

- mérhető úthossz: ~ 3 m (~ 6 m koherenciahossz)

- a rezgések nem nagyon zavarják, azok hatását ki tudja átlagolni

(de azért a rezgésmentes asztal nem hátrány)

Lézeres szögelfordulás mérés:

A mérés pontossága: (λ/8)/s [rad]

pl.: 0,08 μm / 1 m = 8*10^-8 rad

(rezgésmentes környezetben)

Tényleges pontosság 2 szögmásodperc.

2/3600 fok ~ 10^-5 rad

---

[1] Az elektronokra valójában a Fermi-Dirac-statisztika használandó, de esetén a Maxwell-Boltzmann-statisztika is jó közelítés.