Műszaki lézerfizika (GEFIT201B)

2022/2023. tanév 2. félév

Tételek

1. témakör

1.        Az elektromágneses hullámok leírása (hullámegyenlet, síkhullám), összefüggések a hullámjellemzők (φ, ω, f, λ, n) között

2.        Az elektromágneses hullámok intenzitása (w, S, I összefüggései), transzverzalitása és spektruma

3.        A Doppler-effektus. A polarizáció, fázistoló lemezek

4.        Az interferencia, koherencia feltételek, maximális erősítés és gyengítés. Interferométerek

5.        A fény visszaverődése és törése, polarizáció visszaverődésnél és törésnél, a kettős törés.

6.        A diszperzió (színbontás). A teljes visszaverődés, a sarokprizma

7.        Tükrök és optikai lencsék képalkotása, a Kepler-távcső 

8.        A határozatlansági reláció és alkalmazása a minimális nyalábdivergencia és a gerjesztett állapotok élettartamának becslésére

9.        Az abszorpció, a spontán emisszió és az indukált emisszió összehasonlítása, Einstein-féle valószínűségek és összefüggéseik

10.    Erősítés indukált emisszióval, a populációinverzió. A lézerek négy energiaszintje

11.    A lézerek gerjesztésének a módjai. A tükörrezonátor, hatása a lézerfény frekvencia kiszélesedésére

12.    A lézerek longitudinális és transzverzális módusai. A lézerfény legfontosabb tulajdonságai

13.    A lézerek története. Gázlézerek: a He-Ne-lézer

14.    Az argon ion lézer és a CO2 lézer működése

2. témakör

15.    A szilárdtestfizika alapjai, a sávszerkezet, a Fermi-Dirac-statisztika

16.    Szilárdtest lézerek: a rubinlézer, a Nd:YAG lézer működése

17.    A félvezető lézerek működése, heteroátmenetes lézerek

18.    További lézertípusok: szabadelektron lézer, festéklézer, szállézer

19.    Rövid lézerimpulzusok előállítása: aktív és passzív Q-kapcsolás, módusszinkronizáció

20.    A nemlineáris optika alapjai, a frekvencia kettőzés, az ELI ALPS

21.    Lézerbiztonság, a szem károsodása, veszélyességi osztályok

22.    A Bragg-cella, a lézer Doppler rezgésmérés (LDV)

23.    A precíziós lézer-interferometrikus elmozdulás mérés

24.    Az áramlástechnikában alkalmazott lézeres mérési módszerek (LDA, PIV)

25.    A lézeres anyagmegmunkálás alapjai: lézeres vágás, hegesztés, hőkezelés

26.    A holográfia elve és alkalmazásai, sík- és vastag hologramok készítése

27.    Néhány informatikai lézeralkalmazás: CD (DVD), optikai adatátvitel

28.    Lézeres fúzió és hűtés

 

Feladatok

 

1)   Elektromágneses hullám elektromos terét leíró függvény a következő: . Számítsa ki a hullámhosszat, fázissebességet, periódusidőt, a fázisterjedés irányát, a mágneses mező, az EM energiasűrűség és a Poynting-vektor amplitúdóját!

 

2)      Egy vákuumban terjedő lézernyaláb átmérője 1,2mm, az átlagos teljesítménye pedig 5mW. Mekkora a nyaláb intenzitása, az elektromos és mágneses tér csúcsértéke és a fény által okozott nyomás?

 

3)      A 633 nm hullámhosszú vörös fény 45°-os beesési szögben egy 1,33 törésmutatójú vékony szappanhártyára esik. A visszaverődő fénysugarak interferenciája éppen intenzitásmaximumot eredményez. Számítsuk ki a szappanhártya minimális vastagságát!

 

4)      Egy rács 1100 karcolást tartalmaz milliméterenként. Hány fokos szögben vetíti ki a rajta áthaladó látható fény elsőrendű spektrumát? A látható fény hullámhosszhatárait vegyük 430 nm és 680 nm-nek!

 

5)      A CD lemezen a track távolság 1,6 μm. Számítsuk ki, hogy a merőlegesen beeső zöld fény (λ=532 nm) milyen visszaverődési szögekre ad intenzitás maximumot! (19,4°, 41,7°, ~86°)

 

6)      Szappanhártyára (n = 1,33) merőlegesen fehér fény esik. Mekkora legyen a hártya legkisebb vastagsága, hogy visszavert fényben zöldnek (λ=0,5μm) lássuk? (94 nm)

 

7)      Egy rácsnak 20000 vonala van 5,5 cm-en. Adjuk meg azt a fényhullámhosszat, amire a két másodrendű maximum között a szögtávolság 60o! (688 nm)

 

8)      Az 500 nm hullámhosszúságú fénnyel kétréses interferenciaképet hozunk létre az egymástól 0,50 mm távolságú függőleges réspártól 1,5 m-re. Adjuk meg az interferenciamaximumok számát a főmaximum és a tőle balra 1.00 cm-re lévő hely között.

 

9)      Egy domború gömbtükör görbületi sugara 10 cm. Hová helyezzük a tárgyat, ha azt akarjuk, hogy a kép 4 cm távolságra keletkezzen a tükörtől? Szerkesszük meg a képet! (t=0,2 m, a kép látszólagos!)

 

10)    Valamely tárgy 4-szeres lineáris nagyítású képét akarjuk előállítani a tőle 1 m-re elhelyezett ernyőn. Milyen fókusztávolságú vékony lencsét kell használnunk? Mekkorának válasszuk a tárgytávolságot? (f=0,16 m; t=0,2 m)

 

11)    30o-os törőszögű prizmára, egyik oldallapjára merőlegesen, keskeny fehér fénynyalábot ejtünk. A vörös színű fény kilépési pontja és az ernyő merőleges távolsága 20 cm. A prizma anyagának törésmutatója a vörös színű fényre 1,772, az ibolya színű fényre 1,798. Adjuk meg a látható színkép hosszát!

 

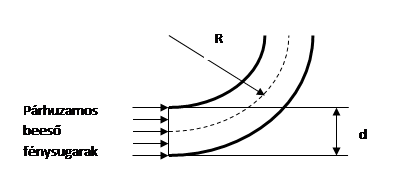
12)    Az ábrán látható optikai szál üvegből készült (n = 1,63) és d = 0,060 mm átmérőjű. Adjuk meg annak az R sugárnak a legkisebb értékét, mellyel a szálat még el lehet hajlítani úgy, hogy a fonal tengelyével párhuzamosan beeső és a szál egész keresztmetszeti területén eloszló sugarakra még mindig fennálljon a teljes visszaverődés feltétele! (0,125 mm)

 

13)    Mekkora a fényképezőgép-objektív gyújtótávolsága, ha a 60m távolságban lévő 15m magas épületről 2mm magasságú valódi képet állít elő a CCD-chipen?

 

14)    A He-Ne lézer 633 nm hullámhosszúságú, a berendezésnél 1 mm átmérőjű nyalábját a Földről a Hold felé irányítjuk.  A határozatlansági reláció alapján becsüljük meg a Holdon megvilágított terület minimális átmérőjét! A Hold - Föld távolságot vegyük 384000 km-nek!  Mekkora kezdeti nyalábátmérő mellett lehetséges elvileg a legkisebb területet a Holdon megvilágítani? Mennyi ekkor a megvilágított folt átmérője?

 

15)    Az emberi szem már alig veszi észre azt a sárga fényt (0,6 mm), amely 1,7×10-6 W teljesítménnyel érkezik a retinához. Hány foton érkezik 1 s alatt a szembe?

 

16)    Egy adott gerjesztett állapot energiája (az alapállapothoz képest) 2 eV, élettartama 10-8 s. Mekkora az alapállapotba történő átmenet során kibocsájtott fotonok hullámhossza és hullámhossz kiszélesedése?

 

17)    Az argonion lézer 514 nm hullámhosszúságú, a berendezésnél 1 mm átmérőjű nyalábjával egy műholdról a Földet pásztázzuk. A határozatlansági reláció alapján becsüljük meg a Földön megvilágított terület minimális átmérőjét, amikor a műhold 200 km magasságban van! Mekkora kezdeti nyalábátmérő mellett lehetséges elvileg a legkisebb területet a Földön megvilágítani? Mennyi ekkor a megvilágított folt átmérője?

 

18)    Egy tárgyat t = 0,8 m távolságra helyezünk el egy D = 5 dioptriás lencsétől. Hol keletkezik a kép, milyen a típusa? Mekkora a nagyítás? Szerkesszük meg a képet! (k=0.2666m, N=1/3)

 

19)    Egy csillámból készült fázistoló lemezben a két polarizációs irányra vonatkozó törésmutató nx=1,594 és ny=1,599. Számítsuk ki egy félhullámú (λ/2) lemez (tehát a két polarizációs irányra π relatív fázistolást végző) vastagságát! (63,3 μm)