9. Fotorealisztikus képszintézis

• Inkrementális képszintézis

• Képminőség vs. számítási idő

• A fizikai modellhez közelebbi számítási mód

• Toy Story

\(\rhd\) Melyek azok az optikai hatások, amelyeket a korábbi, inkrementális képszintézissel körülményes megoldani?

9.1. Sugárkövetés

• raytracing

• 1980-as évek, Andrew S. Glassner

• Képpontonként számol azonos módszerrel

• A fénysugarak útját a kamerától a fényforrásig követi

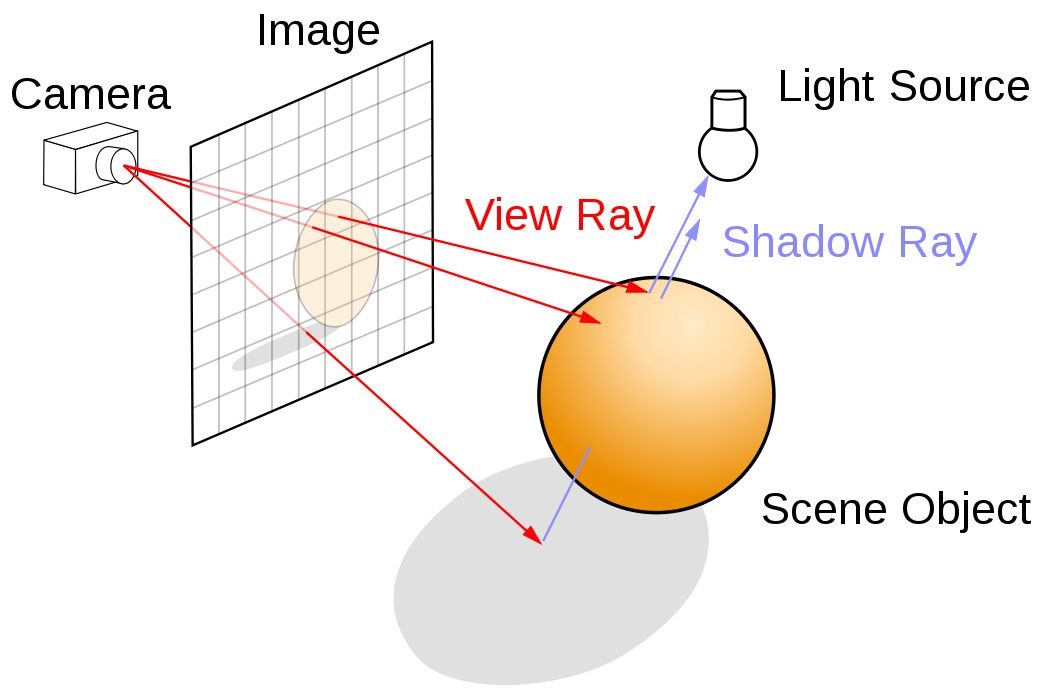
\(\rhd\) Miért előnyösebb a kamerából indítani a fénysugarakat, nem pedig fordítva?

• direkt megvilágítás: A fényforrásból induló fénysugár a felületi pontról visszaverődik, és közvetlenül (direkt módon) a kamerába jut.

• indirekt megvilágítás: A felületi pontról visszaverődő fény egy másik felületi pontot talál el.

A fény visszaverődését figyelembe véve egy rekurzív számításról van szó.

• Meg kell határozni a fénysugár metszéspontját a felületi ponttal.

• Ki kell számítani a felületi normál vektort és a visszaverődési irányt.

• A visszaverődési pontokban lokális megvilágítási modellel számolhatunk.

Megjegyzés

A felületi pontról a visszaverődés jellemzően nem ideális. Eloszlással kellene számolnunk, de a sugárkövető módszer itt egyszerűsíthet.

Megjegyzés

A rekurzió mélységét megadhatjuk paraméterként.

• https://en.wikipedia.org/wiki/Ray_tracing_(graphics)

• https://raytracing.github.io/books/RayTracingInOneWeekend.html

• https://www.scratchapixel.com/lessons/3d-basic-rendering/ray-tracing-overview/light-transport-ray-tracing-whitted.html

9.2. Fény modell

A fénysugár felületi pontról való visszaverődésének pontos leírásához ismernünk kellene a felületet, amelyet azonban csak ideális esetben szoktunk tudni leírni. A fény visszaverődési modelljét emiatt itt is célszerű

• ambiens,

• diffúz

• spekuláris

tagokra bontani (Phong modell).

\(\rhd\) Vizsgáljuk meg 3 különböző irányból érkező fénysugárra a visszaverődő sugarak irányát, eloszlását!

A felületi pontra adódó intenzitást a következőképpen számolhatjuk:

\[I = k_a \cdot i_a + \sum_{m \in M} \left( k_d (\textbf{l}_m \cdot \textbf{n}) i_{m,d} + k_s (\textbf{r}_m \cdot \textbf{v})^{\alpha} \cdot i_{m, s} \right),\]

ahol

• \(M\): a fényforrások (indexeinek) halmaza,

• \(\textbf{n}\): a felületi normálvektor,

• \(\textbf{l}_m\): az \(m\)-edik fényforrásba mutató vektor,

• \(\textbf{v}\): a nézőpontba mutató vektor,

• \(\textbf{r}_m\): az \(m\)-edik fényforrásról való visszaverődés irányának vektora,

• \(k_a, k_d, k_s\): a felületi pont ambiens, diffúz és spekuláris konstansa,

• \(i_a, i_{m,d}, i_{m,s}\): a fényforrások ambiens, diffúz és spekuláris intenzitása,

• \(\alpha\): az anyag csillogósságát leíró konstans (shininess).

A visszeverődési szög az \(m\)-edik fényforrás esetén a következőképpen számítható:

\[\textbf{r}_m = 2(\textbf{l}_m \cdot \textbf{n})\textbf{n} - \textbf{l}_m.\]

• https://en.wikipedia.org/wiki/Phong_reflection_model

• https://en.wikipedia.org/wiki/Bidirectional_reflectance_distribution_functi

9.3. Fénysugarak indítása

A képünk általában téglalap alakú. Kézenfekvő módon a sugarakat egy négyzetrács felbontás szerint indítjuk.

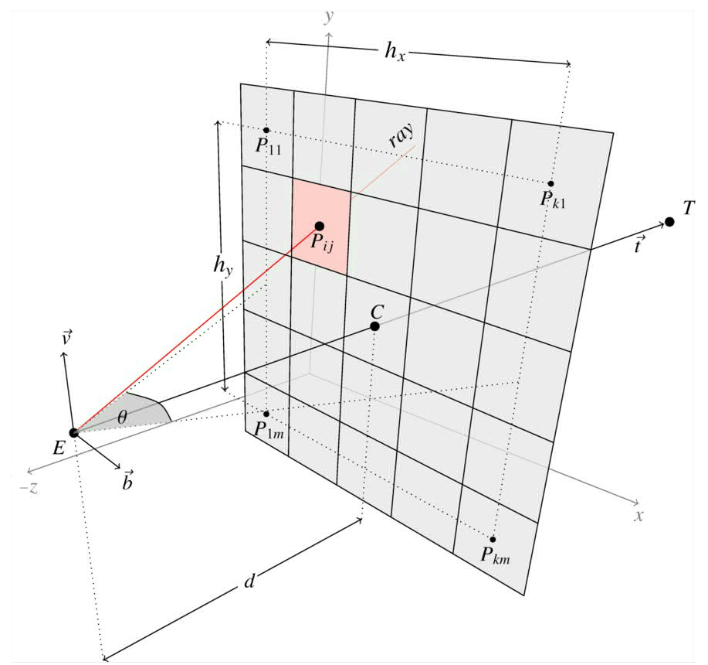
9.4. Metszéspontok számítása

A fénysugár leírásához használjuk a következő paraméteres egyenletet:

\[\textbf{r}(t) = \textbf{s} + t \cdot \textbf{d},\]

ahol

• \(\textbf{s}\): a sugár kiindulópontja,

• \(\textbf{d}\): a fénysugár iránya,

• \(t\): szabad paraméter, \(t \in \mathbb{R}, t \geq 0\).

9.4.1. Háromszög metszése

A számítást két fő lépésben végezhetjük:

• Először megvizsgáljuk, hogy a sugár hol metszi a háromszög síkját, majd

• ellenőrízzük, hogy a metszéspont a háromszögön belül van-e.

Legyenek a háromszög csúcspontjai \(\textbf{a}, \textbf{b}, \textbf{c} \in \mathbb{R}^3\)! Ekkor a háromszög normálvektora:

\[\textbf{n} = (\textbf{b} - \textbf{a}) \times (\textbf{c} - \textbf{a}),\]

helyvektora pedig (például) \(\textbf{a}\).

A metszéspont számításához az \(\textbf{n} \cdot (\textbf{p} - \textbf{a}) = 0\) egyenletet kell megoldani, ahol a \(\textbf{p}\) pont helyére a sugár paraméteres egyenletét írjuk.

• Hogy ha \(t < 0\), akkor a háromszög a sugár mögött van, így nem metszi,

• egyébként az alábbi egyenlőtlenségeket ellenőrízzük:

\[\begin{split}\begin{align} ((\textbf{b} - \textbf{a}) \times (\textbf{p} - \textbf{a})) \cdot \textbf{n} \geq 0, \\ ((\textbf{c} - \textbf{b}) \times (\textbf{p} - \textbf{b})) \cdot \textbf{n} \geq 0, \\ ((\textbf{a} - \textbf{c}) \times (\textbf{p} - \textbf{c})) \cdot \textbf{n} \geq 0. \\ \end{align}\end{split}\]

Megjegyzés

A számítás közben a felületi pont normálvektorát is megkaptuk.

9.4.2. Gömb metszése

Jelöljük a gömb középpontját \(\textbf{c} \in \mathbb{R}^3\) vektorral, a sugarát pedig \(R \in \mathbb{R}\) betűvel. A gömb egyenlete a következőképpen írható fel:

\[|(\textbf{s} + t \cdot \textbf{d}) - \textbf{c}|^2 = R^2.\]

Ezt megoldva az alábbi egyenletet kapjuk:

\[(\textbf{d} \cdot \textbf{d}) t^2 + (2 \cdot \textbf{d} \cdot (\textbf{s} - \textbf{c})) t + ((\textbf{s} - \textbf{c}) \cdot (\textbf{s} - \textbf{c}) - R^2) = 0.\]

• Akkor lesz metszéspontunk, hogy ha \(t \geq 0\), és

• két metszéspont esetén a kisebb \(t\) értékhez tartozót választjuk.

Jelöljük a metszéspontot \(\textbf{p}\)-vel! Az egység hosszúságú normálvektort a következőképpen számíthatjuk ki:

\[\textbf{n} = \dfrac{\textbf{p} - \textbf{c}}{|\textbf{p} - \textbf{c}|}.\]

9.4.3. Általános felületek metszése

Egy \(F(x, y, z) = 0\) implicit felület esetén az

\[F(s_x + d_x \cdot t, s_y + d_y \cdot t, s_y + d_y \cdot t) = 0\]

egyenlet megoldására van szükség. A felülettől függően ez általában egy nemlineáris egyenlet megoldását teszi szükségessé.

Tekintsünk egy \(\textbf{f}(u, v) \in \mathbb{R}^3\) felületet! A sugárral való metszéshez az

\[\textbf{f}(u, v) = \textbf{s} + t \cdot \textbf{d}\]

egyenlet megoldására van szükség, amelyből a \(t, u, v\) paramétereket kapjuk meg. Ebben az esetben is csak akkor beszélhetünk metszéspontról, hogy ha \(t \geq 0\), továbbá, hogy ha az \((u, v)\) paraméterek a megengedett tartományon vannak.

9.4.4. Gyorsítási lehetőségek

Segédstruktúrák és előszámítások használatával gyorsíthatjuk a metszéspontok meghatározását.

• Háromszögek esetében élhetünk a triviális lapeldobás lehetőségével (amelyet itt az aktuális sugár irányára kell elvégeznünk).

• Az objektumainkat befoglaló testekbe (bounding box) tehetjük, melyekre a metszésszámítás gyorsan elvégezhető. (Ez lehet például téglatest vagy gömb.)

• Rekurzívan feloszthatjuk a teret kisebb részekre, és így hierarchikusan végezhetjük a metszés számítást (oktális fa, octal tree).

\(\rhd\) Egy program optimalizálása során milyen lépéseket érdemes követni?

9.5. Élsimítás

A mintavételezésből adódóan a kapott képen csipkésedést tapasztalhatunk, a kapott kép pixeles lesz (aliasing). A javításához élsimító módszereket (Anti-aliasing) használhatunk.

Néhány lehetséges megoldás például az alábbi.

• Növelhetjük a sugarak indításához használt rács felbontását, majd a kapott, nagyobb felbontású képet visszaátlagolhatjuk az eredeti felbontásra.

• A képpontokon belül véletlenszerűen mintavételezhetünk.

9.6. Globális illumináció

A korábbi, egyszerűbb modellek esetében az alábbi feltételezésekkel éltünk.

• A fénysugár egy adott irányba verődik vissza.

• A fényforrásaink pontszerűek.

• A fénysugár a felületből kifelé verődik vissza.

• A fény RGB összetevőkből áll össze (tehát nem vettük figyelembe a teljes hullámhossztartományt).

Ezek egyszerűsítették a számításainkat, viszont a természetben a fény nem így működik. A globális illuminációs modell egy, a fény fizikai természetéhez közelebbi modellt igyekszik adni.

• https://en.wikipedia.org/wiki/Global_illumination

\(\rhd\) Tegyük fel, hogy elindítunk egyetlen sugarat, és 5 rekurziós szinten, minden lépésben 8 felé szóródik a fénysugarunk! Az utolsó rekurziós szinten mennyi lesz a sugarak száma?

A fény mennyiségének eloszlását gömbi koordinátarendszerben, egy gömb felületén tekintjük.

Megjegyzés

A teljes gömb önmagában alkalmas lenne a felületen belüli fényvisszaverődés kezelésére, de egyszerűbb azt az esetet külön kezelni.

Jelöljük a gömbi koordinátarendszer két szögét \(\varphi\) (azimuth) és \(\vartheta\) (elevation) betűkkel!

Az egyes irányokhoz tartozó ponthalmazok méretét számszerűsíteni szeretnénk. Ehhez bevezethetjük a térszög (solid angle) fogalmát, amely az adott irányhoz tartozó területet adja meg az egységsugarú gömb felületén. Jelölése: \(\Omega\), mértékegysége sr (szteradián).

A globális illuminációs modellek azt vizsgálják, hogy a felületen milyen a fény eloszlása.

• Mivel folytonos tér közelítéséről van szó, ezért az összefüggések alapvetően integrálos alakban adhatók meg.

• Jellemzően véges számú fotonnal való szimulációról van szó, amelyhez így mintavételezni kell.

9.7. Szoftverek

• https://en.wikipedia.org/wiki/List_of_ray_tracing_software

9.7.1. POV-Ray

• Persistence of Vision Raytracer

• https://en.wikipedia.org/wiki/POV-Ray

9.7.2. LuxCoreRender

• Physically Based Renderer

• https://luxcorerender.org/

• https://en.wikipedia.org/wiki/LuxCoreRender

9.7.3. Blender

• Modellező szoftver, de renderelésre is alkalmas

• https://www.blender.org/