Rövid történeti betekintést adunk a Miskolci Egyetem, Matematikai Intézet Analízis Tanszéke tevékenységéről. Bemutatjuk a Tanszék jelenlegi legfontosabb oktatási- és kutatási eredményeit. Megadjuk az utóbbi 10 évben a Tanszék oktatói által írt jegyzetek, tankönyvek listáját. Részletesebben tárgyaljuk a Differenciálegyenletek elméletében elért eredményeket a Numerikus-analitikus módszerek területén.
1. Rövid történeti betekintés az Analízis Tanszék tevékenységébe
Az 1999-es év, nemcsak a Miskolci Egyetem és Gépészmérnöki Karának, hanem az egyetem matematikusainak is miskolci székhellyel való oktatási- és tudományos tevékeny-ségének 50. évfordulója.
Az egyetem fennállásának 264 éves történetében - 1735-től a Selmeci Akadémián, 1919-től Sopronban, 1949-től a Nehézipari Műszaki Egyetem miskolci székhellyel történő alapításától kezdődően, majd 1990-ben a Miskolci Egyetem névre való átnevezés után - a matematikusok hathatós részt vállaltak nemcsak az oktatásban, kutatásban, hanem az egész intézménynek a kiépítésében is.
Az Analízis Tanszék az 1975-ben megalakult Matematikai Intézeten belül működik. Alapításának éve 1975, jogelődje az 1949-ben létrehozott Matematikai Tanszék. Ismeretes, hogy a Matematikai Tanszék a jelenlegi Földes Ferenc Gimnázium épületében kezdte meg oktatását, majd 1952-ben költözött az Egyetemvárosba, ahol mai helyét az A/4 épületben 1965-ben foglalta el.
A Matematikai Intézet és az Analízis Tanszékének előző vezetői:
1949-1950: a Matematikai Tanszék vezetője: Dr. Borbély Samu mérnök, matematikus,
egyetemi tanár, akadémius;
1950-1952: két Matematikai Tanszék működött:
Matematika I. vezetője: Dr. Borbély Samu;
Matematika II. vezetője: Dr. Aczél János, okl. matematika-fizika szakos
tanár, matematikai tudomány kandidátusa, egyetemi tanár, a Kanadai
Tudományos Akadémia tagja és az MTA külső tagja;
1952-1975: újra egy Matematikai Tanszék működött:
1952-1955: tszv.: Dr. Borbély Samu;
1955-1974: tszv.: Dr. Gáspár Gyula okl. matematika-fizika szakos tanár, egyetemi tanár,
a matematikai tudomány kandidátusa;
1974-1975: mb.tszv.: Dr. Szarka Zoltán, okl. mérnök, egyetemi docens;
1975: a Matematikai Intézet létrehozása az Analízis és Számítástechnikai
tanszékekkel (melynek neve 1990-ben Alkalmazott Matematikai Tanszékre
változott).
A Matematikai Intézet igazgatói:
1975-1983: Dr. Vincze Endre, okl. gépészmérnök, egyetemi tanár, a matematikai
tudomány kandidátusa;
1983-1985: mb. igazgató: Dr. Szintay István, okl. gépészmérnök, egyetemi tanár, a
közgazdaságtudomány kandidátusa;
1985-1988: Dr. Maurer Gyula okl. matematikus, egyetemi tanár, a matematikai
tudomány kandidátusa;
1988-1991: Dr. Páczelt István okl. gépészmérnök, egyetemi tanár, akadémikus;
1991- Dr. Galántai Aurél, okl. matematikus, a matematikai tudomány kandidátusa,
dr. habil., egyetemi tanár;
Az Analízis Tanszéke vezetői:
1975-1978: Dr. Szarka Zoltán;
1978-1988: Dr. Vincze Endre;
1988-1991: Dr. Szarka Zoltán;
1991-1997: Dr. Kálovics Ferenc okl. matematika-fizika szakos tanár, egyetemi docens, a
matematikai tudomány kandidátusa;
1997- Dr. Rontó Miklós okl. matematikus, egyetemi tanár, a matematikai tudomány
doktora.
A Miskolci Egyetem Közleményeinek Természettudományi sorozata egy külön számban [1] emlékezik meg a Tanszék első két tanszékvezető professzoráról Dr. Borbély Samu akadémikusról és Dr. Gáspár Gyula egyetemi tanárról. Ez a külön kiadvány emléket állít még egy neves matematikusnak - aki Miskolcon a Matematikai Tanszéken jutott el a matematikai tudomány doktora tudományos fokozathoz és a professzori címhez, a nagyon fiatalon elhunyt - Dr. Hosszú Miklósnak (1929-1980).
Az életrajzokat egyetemünk 3 már nyugállományú oktatója állította össze, a rájuk jellemző alapossággal, pontossággal és szeretettel. Dr. Borbély Samu akadémikusról, Dr.h.c., dr. Terplán Zénó akadémikus professzor emlékezik meg. Dr. Gáspár Gyula professzor emlékét Dr. Szarka Zoltán egyetemi docens örökítette meg. Dr. Hosszú Miklós oktatói és tudományos életútját Dr. Salánki József egyetemi adjunktus mutatta be, aki mind a Matematikai Tanszéken, mind 1972-től a Gödöllői Agrártudományi Egyetemen közeli munkatársa volt a professzornak. Az előszót a szóbanforgó kiadványhoz ezen sorok szerzője írta.
1.1. A Tanszék oktatói a jubileumi 1999-es évben
Az Analízis Tanszék oktatói és kutatói az 50. jubileumi évben:
Dr. Bukszár József okl. matematikus, PhD, egyetemi tanársegéd;
Dr. Csernyák László okl. matematika-fizika szakos tanár, a matematikai tudomány kandidátusa, egyetemi tanár (mellékállásban);
Dr. Kálovics Ferenc okl. matematika-fizika szakos tanár, a matematikai tudomány kandidátusa, egyetemi docens;
Dr. Kovács Béla okl. gépészmérnök, a műszaki tudomány kandidátusa, egyetemi docens; Körei Attila okl. matematikus, egyetemi tanársegéd;
Dr. Körtesi Péter okl. matematikus és matematika szakos tanár, főiskolai docens;
Dr. Mészáros József okl. gépészmérnök, egyetemi adjunktus;
Dr. Raisz Péterné dr. okl. matematika-fizika szakos tanár, PhD, egyetemi adjunktus;
Dr. Radeleczki Sándor okl. matematikus és matematika szakos tanár, a matematikai tudomány kandidátusa, egyetemi docens;
Dr. Rontó Miklós okl. matematikus, a matematikai tudomány doktora, egyetemi tanár;
Dr. Simon Károly okl. matematikus, a matematikai tudomány kandidátusa, egyetemi docens;
Dr. Szalontai István okl. matematika-fizika szakos tanár, főiskolai docens;
Dr. Szigeti Jenő okl. matematikus dr. habil, a matematikai tudomány kandidátusa, egyetemi tanár;
Tóth Lajosné Dr. Tuzson Ágnes okl. gépészmérnök, PhD, egyetemi docens;
Vadászné Dr. Bognár Gabriella okl. gépészmérnök, a matematikai tudomány kandidátusa, egyetemi docens;
Dr. Vincze Endre okl. gépészmérnök, a matematikai tudomány kandidátusa, egyetemi tanár.
1.2. Oktatási terület
Az Analízis Tanszék a Miskolci Egyetem Bányamérnöki, Gazdaságtudományi, Gépészmérnöki és Kohómérnöki Karain az alábbi szintű képzési területeken oktat:
- egyetemi szintű nappali tagozatos képzés mind a 4 karon;
- főiskolai szintű képzés a Gépészmérnöki Kar nappali és levelező tagozatán, ill. a
Gazdaságtudományi Kar levelező tagozatán;
- idegennyelvű önköltséges képzés a Bányamérnöki és Gépészmérnöki Karokon;
- a PhD programokban mind a 4 karon.
A tanszék oktatási tevékenysége számos szakterületre terjed ki:
- egyetemi szintű Gépészmérnöki Szak, nappali tagozat (1998-ban a felvett hallgatók száma 238 fő);
- egyetemi szintű Műszaki informatika Szak, nappali tagozat (1998-ban 101 hallgató nyert felvételt);
- egyetemi szintű Műszaki menedzser Szak, nappali tagozat (1998-ban 100 elsőéves); - főiskolai szintű Gépészmérnöki Szak, nappali tagozat (1998-ban 49 új hallgató); - főiskolai szintű Villamosmérnöki Szak, nappali tagozat (1998-ban 60 elsőéves); - főiskolai szintű Gépészmérnöki Szak ill. Villamosmérnöki Szak, levelező tagozat (költségtérítéses, 1998-ban összesen 301 elsőéves);
- főiskolai szintű Műszaki Szakoktatói Szak (költségtérítéses, 1998-ban 40 fő nyert felvételt);
- a Gépészmérnöki Kar 0-adik évfolyama 1995-1998-ig (költségtérítéses, évente kb. 20 fő);
- egyetemi előkészítő tanfolyam 1998-ig (költségtérítéses évente mintegy 30 fő);
- Gazdaságtudományi Kar 0-adik évfolyama 1998-ig (költségtérítéses, évente kb.
50 fő).
Az általunk oktatott 35 tárgy az alábbi nagyobb tantárgycsoportokba sorolható:
- Differenciál- és integrálszámítás;
- Vektoranalízis;
- Differenciálegyenletek;
- Komplex függvénytan;
- Funkcionál-analízis és variációszámítás;
- Integrálegyenletek;
- Speciális függvények;
- Lineáris algebra;
- Diszkrét matematika;
- Formális nyelvek;
- Gazdaságmatematika.
A matematika oktatásának fokozatos bővülése következtében az Analízis Tanszék heti óraszáma az I. félévben mintegy 55 óra előadás és 218 óra gyakorlat, a II. félévben közel 35 óra előadás és 140 óra gyakorlat. Említésre méltó, hogy a Tanszék az őszi félévben 1900, míg a tavasziban 1700 hallgatót oktat.
A PhD képzézs keretében a Tanszék a
- Differenciál- és integrálegyenletek;
- Speciális függvények;
- Modern analízis;
- Funkcionálanalízis elemei;
- Valószínűségszámítás és Matematikai statisztika elemei;
- Diszkrét matematika
tárgyakat oktatja az egyetem 4 karán.
A Tanszéken 4-en nyertek el Széchenyi Professzori Ösztöndíjat (Kovács Béla,
Rontó Miklós, Simon Károly, Szigeti Jenő) és 2 oktató Bolyai ösztöndíjban részesült (Vadászné Bognár Gabriella, Radeleczki Sándor).
1.3. Jegyzet és könyvírás
A Tanszék oktatói szerzői ill. társszerzői az utóbbi években megjelent alábbi jegyzeteknek, tankönyveknek:
Külön kiemelést érdemel a Publications of the University of Miskolc, Series D, Natural Sciences, Mathematics angol nyelvű matematikai külön füzetének létrehozása és rendszeres kiadása, melyre az Analízis és Alkalmazott Matematikai Tanszékek kaptak megbízást. Eddig megjelent 5 kötet: vol. 36, fasc. 1 (1995), vol. 36, fasc 2 (1996), vol 37 (1997, vol. 38 (1998), vol. 39 (1999).
1.4. Fontosabb kutatási eredmények
A Tanszéknek a következő hazai és nemzetközi intézményekkel van kutatói kapcsolata: MTA Matematikai Kutató Intézet, ELTE, BME, KLTE, JATE, Bolyai János Matematikai Társulat, Kievi Tudományegyetem (Ukrajna), Ukrán TA Matematikai Kutató Intézete (Ukrajna), Universita di Palermo (Olaszország), CWI - Centrum voor Wiskunde en Informatica (Hollandia), University of St. Andrews (Skócia), University of Edinburgh (Skócia), Kolozsvári Babes Bolyai Tudományegyetem (Románia), Societé European pour la Formation des Ingenieurs (SEFI) Matematikai Munkacsoportja (Anglia), Technical University of Darmstadt (Németország), Ungvári Tudományegyetem (Ukrajna).
Ezek a kapcsolatok bizonyos mértékben hozzájárultak ahhoz, hogy a Tanszék jelenlegi kutatási irányai a Differenciálegyenletek elmélete, Dinamikus rendszerek, Algebra és Diszkrét matematika, Intervallumanalízis, Függvényegyenletek.
Az utóbbi évek fontosabb kutatási eredményei:
- Konstruktív numerikus-analitikus módszerek kidolgozása közönséges- és parciális differenciálegyenletek, peremérték-feladatainak vizsgálatára. (Rontó Miklós, Vadászné Bognár Gabriella, Raisz Péterné, Tóth Lajosné Tuzson Ágnes, Kovács Béla, Mészáros József,);
- Sima dinamikai rendszerek elméletének fejlesztése (Simon Károly, Körei Attila); - Algebrai struktúrák, a Gyűrű- és hálóelmélet továbbfejlesztése (Szigeti Jenő, Radeleczki Sándor, Körtesi Péter);
- Intervallumanalízisbeli módszerek megalapozása nemlineáris feladatok megoldására (Kálovics Ferenc, Mészáros Józsefné).
A Tanszék oktatói az utóbbi években 6 OTKA, 2 FEFA, 2 FPP és 1 OMFB kutatási projektben vettek részt.
Az Analízis Tanszék az utóbbi években a következő tudományos rendezvényeket szervezte, illetve részt vett azok szervezésében az Intézet Alkalmazott Matematikai Tanszékével közösen.
- 6th International on Numerical Methods, Miskolc, 1994.aug. 22-26. Résztvevők száma: 100. Szervező Bizottság elnöke: Dr. Galántai Aurél.
- Conference on Numerical Methods and Computational Mechanics, Miskolc, 1996 július 15-19. Résztvevők száma: 110. Szervező Bizottság elnöke: Dr. Galántai Aurél.
- Ring Theory Conferencia, 1996 Miskolc, Hungary, July 15-20. A satelite conference of the Second European Congress in Mathematics (Budapest, July 21-27, 1996) Résztvevők száma: 198. Szervező Bizottság tagja: Dr. Szigeti Jenő.
- Junior Mathematical Congress'96, Miskolc, 1996. július 29- aug. 2. Résztvevők száma: 340. Szervező Bizottság elnöke: Dr. Körtesi Péter.
- Mathematical Camp and Junior Mathematical Conference'97, Miskolc 1997. aug. 17-23. Résztvevők száma: 110. Szervező Bizottság elnöke: Dr. Körtesi Péter.
- Conference on dimensions and dynamics'98. Miskolc, 1998. július 2-24. Résztvevők száma: 42. Szervező Bizottság elnöke: Dr. Simon Károly.
- Conference on Numerical Methods and Computational Mechanics, Miskolc 1998.aug.24-27. Résztvevők száma: 126. Szervező Bizottság elnöke: Dr. Galántai Aurél.
A Matematikai Intézet (és ennek keretében az Analízis Tanszék) kutatási tevékeny-sége az 1949-1989 közötti időszakban a Nehézipari Műszaki Egyetem miskolci székhellyel való működésének és a Gépészmérnöki Kar alapításának 40 éves Jubileumi Tudományos ülésszakán elhangzott előadásokban illetve a Kar és Tanszékeinek szentelt külön kiadványban [2] kerültek bemutatásra, eléggé általános formában.
Az 50-es évek végétől a 70-es évek elejéig az akkori Matematikai Tanszéken, mint a [2] kiadványban olvasható, a Függvényegyenletek témakörében folytatódtak a legaktívabb kutatások. Ezen a szakterületen 1966-ban, 1968-ban és 1970-ben a Tanszék 3 sikeres nemzetközi kollokviumot szervezett, illetve aktív résztvevője volt a sárospataki Függvényegyenletek c. nemzetközi konferenciáknak.
A későbbiekben a tanszéki kutatások súlypontja a Differenciálegyenletek, az Operációkutatás ill. a Numerikus módszerek felé tolódott el. Az 1980-as évek elejétől a tanszéken az algebrai kutatások foglalnak el vezető szerepet.
Megjegyzésre érdemes, hogy a műszaki alkalmazások állandóan jelen voltak és vannak a tanszék kutatási tevékenységében.
A Publications of the University of Miskolc, Series D, Mathematics v. 39 (1999) kötetben az Alkalmazott Matematikai Tanszéken a numerikus módszerekben elért eredményeket bemutató - Galántai Aurél professzor által írt - dolgozat mellett, a Tanszékünkön folyó algebrai és gyűrűelméleti vizsgálatokat Szigeti Jenő professzor és az intervallumanalízisbeli kutatásokat Dr. Kálovics Ferenc egyetemi docens külön cikkben foglalja össze. A dinamikus rendszerek, illetve a parciális differenciálegyenletek területén kapott új eredményeit Dr. Simon Károly egyetemi docens, illetve Vadászné Dr. Bognár Gabriella egyetemi docens ugyanabban a kötetben adja közre.
A továbbiakban ez a kiadvány a Tanszéken az utóbbi években a Differenciál-egyenletek témakörében elért eredményeket mutatja be.
2. A differenciálegyenletek területén elért kutatási eredmények
A differenciálegyenletek területén a peremérték-feladatokkal foglalkozó fejezetek esnek a legközelebb a gyakorlati alkalmazásokhoz. Ezek a feladatok állítják elő számos esetben azoknak a jelenségeknek, folyamatoknak a matematikai modelljeit, melyeket időbeli és térbeli változás, fejlődés és dinamika jellemez.
Az általunk folytatott kutatások a különböző nemlineáris közönséges differenciál-egyenlet-rendszerekhez rendelt peremérték-feladatok megoldásainak egzisztencia vizsgála-tára illetve meghatározására vonatkoztak. Ezen célok elérésére megfelelő numerikus-analitikus eljárásokat dolgoztunk ki és továbbfejlesztettük a kollokációs módszert.
2.1. Numerikus-analitikus módszerek nemlineáris peremérték-feladatok
vizsgálatában
Rontó Miklósnak 1992-ben a Miskolci Egyetemre való meghívása után az Analízis Tanszéken is létrejött egy kutatócsoport, amely bekapcsolódott az általa kezdeményezett és irányított kutatásokba a differenciálegyenletek peremérték-feladatainak területén az ún. numerikus-analitikus módszerek elméletének egyes témaköreibe.
Egy pár évtizede Samoilenko A.M. akadémikus professzorral közösen kifejlesztett , sorozatos közelítéseken alapuló numerikus-analitikus módszerek csoportja azon kisszámú eljárások közé tartozik, melyek konstruktív lehetőséget adnak a közönséges differenciál-egyenletek különböző típusú (periodikus, kétpontos, többpontos, határozott integrált tartalmazó peremfeltételek melletti és impulzusos feladatok) nemlineáris peremérték-feladatok megoldásainak vizsgálatára, mind egzisztencia, mind a közelítő megoldás előállítása szempontjából.
Korábban a szerzőnek ebben a témakörben elért eredményei három társszerzős orosz és egy angol nyelvű monográfiában: Samoilenko A.M. és Ronto N.I. [3-6] illetve számos szakdolgozatban [pl. 8,10-15,18] kerültek ismertetésre. Az említett könyvek doktorandusz és egyben matematikus szakos hallgatóknak szóló tankönyvekként is alkalmazhatók speciális kollégiumok oktatására.
A szóbanforgó témakörben az Analízis Tanszéken elkezdett kutatások eredményes-ségét mindennél jobban jelzi, hogy oktatóink az utóbbi időben mintegy 17 hazai és nemzetközi konferencián adták elő kutatási eredményeiket, illetve 39 dolgozatot publikáltak, melyek felsorolásra is kerülnek az irodalomjegyzékben.
A továbbiakban, megfelelő csoportosítással, ezen tanulmányokban elért legfontosabb eredmények rövid bemutatására kerül sor, melyeket megpróbálunk összevetni a már ismertekkel.
Elöljáróban bemutatjuk a numerikus-analitikus módszer (NAM) alapgondolatát. A módszer alapelve szerint az adott peremérték-feladat (PÉF) helyett minden esetben egy megfelelően "perturbált" feladatot állítunk elő (csak a differenciálegyenletrendszer módosul, a peremfeltételek változatlanok). A módosított PÉF bizonyos számú szabad paramétert tartalmaz, melyek számbeli értékét egy algebrai vagy transzcendens egyenletrendszer megoldásaként kapjuk.
Megjegyezzük, hogy a sorozatos közelítésen alapuló NAM absztrakt sémája és alapgondolata a [3,4,6] monográfiákban, Rontó M. [43] dolgozatában illetve a "The Second World Congress of Nonlinear Analysts" (Athens, 1996) kongresszus szekciójának plenáris előadásában került bemutatásra a következő operátor alakban felírt egyenlet és peremfeltételek esetén:
(1)
Ebben a feladatban 
zárt korlátos tartomány és C(D) az
folytonos m -változós n -dimenziós vektorfüggvények tere a D tartomány felett. Továbbá K(D) a C(D) azon alterét jelöli, amely az
absztrakt peremfeltételt kielégítő függvényekből áll. Így a feladat az 
egyenletnek az absztrakt peremfeltételt kielégítő 
megoldásnak az egzisztencia vizsgálatából illetve meghatározásából áll.
Ahhoz, hogy a fixpont alakú egyenletet a K(D) altérben valamilyen sorozatos közelítés módszerével vizsgáljuk, fenn kell állnia az 
relációnak. Általában ez a feltétel nem teljesül, következésképpen célszerű az A operátor mellett bevezetni egy bizonyos értelemben hozzá "közel eső" 
operátort, amelyiknek mind értelmezési tartománya, mind értékkészlete K(D) -beli. Ezek után már egy másik
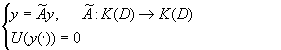(2)
"perturbált" peremérték-feladatot tekintünk. Az operátort alkalmasan úgy kell bevezetni, hogy teljesüljenek a következő feltételek:
a) az (1) PÉF minden megoldása a módosított (2) PÉF -nak is megoldása;
b) az új (2) PÉF minden olyan y megoldása, amelyre teljesül egy bizonyos
(3)
mellékfeltétel, egyben az eredeti (1) PÉF megoldását adja;
c) az ún. "meghatározó" (3) egyenletet úgy választjuk meg, hogy az adott (1) PÉF összes megoldása kielégítse.
Mivel az operátor a K(D) teret önmagába képezi le, megkísérelhetjük a (2) PÉF megoldását az
(4)
iterációs módszer használatával keresni.
Az 
kezdeti approximáció bizonyos szabadságfokkal rendelkezik. Speciálisan tekinthetjük úgy, mint paraméterektől függő függvényt, vagy egyszerűen egyenlővé tehetjük egy n -dimenziós paraméter-vektorral.
Nyilvánvaló, hogy a (4) szukcesszív approximációk és határfüggvénye is függnek az paramétertől:
, (5)
és ezen függvények mindegyike eleve kielégíti az adott peremfeltételt az paraméter minden értékére.
Továbbá a 
meghatározó egyenlet 
megoldása megadja az eredeti (1) PÉF 
megoldásához tartozó paraméter értékeit.
Megjegyezzük, hogy a 
"közelítő" meghatározó egyenlet 
megoldása pedig az (1) PÉF 
közelítő megoldásához vezet.
A szóbanforgó sorozatos közelítésen alapuló numerikus-analitikus módszerben analitikus technikát használunk az (5) közelítések meghatározására és numerikusat a (3) meghatározó (vagy közelítő meghatározó) egyenlet megoldására.
Az egzisztencia vizsgálat a meghatározó (vagy közelítő meghatározó) egyenletrendszer tanulmányozásával illetve a közelítő megoldások tulajdonságainak figyelembevételével történik.
A numerikus-analitikus módszerekkel kapcsolatban a következő általános elméleti és gyakorlati problémák merülnek fel:
a) az A operátor alapján a megfelelő 
operátor alakjának kidolgozása;
b) a meghatározó (3) egyenletben szereplő B operátor minél egyszerűbb felírása;
c) hatékony elégséges feltételek előállítása az (5) sorozatos közelítések konvergenciájára;
d) a magasabbrendű 
közelítések konstruktív meghatározása;
e) a meghatározó (vagy közelítő meghatározó) egyenletrendszer effektív numerikus megoldása;
f) könnyen ellenőrizhető hibabecslések megalapozása.
Amint az absztrakt sémából is kiderül a NAM alkalmazhatósági szempontból eléggé univerzális tulajdonságokkal rendelkezik. Azonban, konkrét esetekben a módszer algoritmusának kidolgozása és megalapozása során nyilvánvaló, hogy figyelembe kell venni az adott differenciálegyenlet tulajdonságait (pl. típusát, rendjét, explicit vagy implicit alakját, együtthatóinak periodicitását, Banach-térbeli tulajdonságait) illetve az adott peremfeltételek alakját (periodikus, kétpontos, három-vagy többpontos, interpolációs típusú, határozott integrált tartalmazó feltétel, nemlineáris mellékfeltétel). Valószínűleg ez a magyarázata annak, hogy a numerikus-analitikus módszer fejlesztése több irányban is történik.
Az első irányzat: a módszer kidolgozása a nemlineáris differenciálegyenletek újabb osztályaira (másodrendű differenciálegyenletek, retardált, - funkcionál egyenletek) különböző típusú peremfeltételek mellett.
A második irányzat: a NAM alkalmazhatósági feltételeinek kibővítése és azok finomítása.
A harmadik irányzat: az eljárás általánosítása paramétert tartalmazó feladatokra (kvázi sajátérték-feladatokra) illetve absztrakt terekben értelmezett PÉF esetén.
A negyedik irányzat: a magasabbrendű közelítések előállítását megkönnyítő módosítások kifejlesztése (polinomiális közelítések, szimbolikus számításokra alkalmas programcsomagok felhasználása, kettős iterációs eljárás megalapozása).
Az ötödik irányzat: a módszer alapelvének figyelembevételével újabb numerikus-analitikus technikák kidolgozása.
Kutatásaink az első négy irányzatot érintették. A továbbiakban ebben a témakörben a elért legfontosabb eredményeink kerülnek bemutatásra.
A NAM újabb változatainak segítségével Ronto M. és Tégen R. M. [22], Tégen R.M. [28] dolgozataiban megoldották a
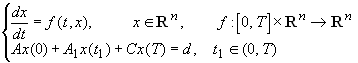(6)
alakú hárompontos nemlineáris PÉF - ok széles osztályának egzisztencia problémáját és ebben eljárást is adtak a közelítő megoldás meghatározására. Olyan elégséges egzisztencia feltételeket állítottak elő, amelyekben explicit módon figyelembe vették mind az adott differenciálegyenlet-rendszer mind a peremfeltételek tulajdonságait. Érdekesség, hogy a korábban Ronto M. és Savina T.V. [23] cikkében kifejlesztett NAM nem volt alkalmas a (6) alakú PÉF kezelésére, ha a peremfeltételekben az 
mátrixok külön-külön szingulárisak. A [22,28] dolgozatokban az utóbbi megszorítást sikerült kiküszöbölni, ha találhatók olyan 
állandók, melyekre
.
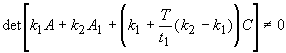Samoilenko A.M. és Ronto N.I. [6] monográfiájában ismertetett kétpontos polinomiális verzióból kiindulva, Rontó M. és Tégen R.M. [25,44,46], Tégen R.M. [36,37] cikkeikben kifejlesztették a (6) hárompontos PÉF-ra vonatkozó numerikus-analitikus módszer polinomiális változatát. Ez azt jelenti, hogy az (5) sorozatos közelítésekből származtatott eddigi 
függvények helyett speciális p -edfokú polinomiális 
közelítéseket alkalmazunk. Ez az egyik lehetőség a magasabbrendű közelítések és a magasabbrendű közelítő meghatározó egyenlet konstruktív előállítására, illetve ezeknek az egzisztencia vizsgálatban való felhasználására. Ezentúl kidolgoztunk egy mátrix-vektor műveletrendszert, mely lényegesen egyszerűsíti a polinomiális közelítések együtthatóinak meghatározását.
A NAM második fejlesztési irányzatához tartozó témakörrel, azaz az alkalmazhatósági feltételek kibővítésével és azok finomításával foglalkozik Rontó M. és Mészáros J. [33] dolgozata. Ebben a cikkben megadtuk a NAM két alapvető lemmájának egy új, módosított változatát. Ezek a segédállítások lényegesek mind a közelítő megoldások konvergenciájának bizonyításában, mind az egzisztencia vizsgálatoknál illetve hiba-becsléseknél.
Így például a
differenciálegyenlet esetén, ha az
egyenlőtlenségek teljesülnek, akkor az ismert
(7)
alkalmazhatósági feltételben sikerült a q konstanst 
-ra javítani. Összehasonlításként megemlítjük, hogy Samoilenko A.M. 1966 -os eredeti dolgozatában és a [3,4] könyvekben 
az [5,6] monográfiában 
, Kwapisz M. 1992 -es cikkében 
.
Idevonatkozóan megjegyezzük, hogy Rontó M., Ronto A. N. és Trofimchuk S.I. [39] dolgozatában a sorozatos közelítések konvergenciája bizonyítást nyert (nem az említett lemmák segítségével), ha a (7) feltételben 
.
Samoilenko A.M., Ronto N.I. és Martinyuk S.V. [11] cikkében a NAM megalapozása olyan nemlineáris PÉF esetén található meg, amikor az adott peremfel-tételekben határozott integrált tartalmazó tagok szerepelnek.
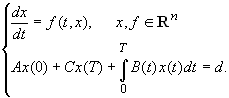
Ronto M. és Martinyuk O.M. [12] dolgozatában a NAM olyan változata kerül kidolgozásra, mely megszámlálhatóan végtelen sok másodrendű nemlineáris differenciálegyenlet-rendszer
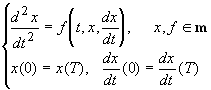
T -periodikus megoldásának vizsgálatára és meghatározására alkalmas (elsőrendű differenciálegyenlet-rendszerre való visszavezetés nélkül).
Kifejlesztettük a numerikus-analitikus módszer változatait paramétereket tartalmazó feladatokra is. Így Rontó M. és Korol I.I. [24] cikkében a
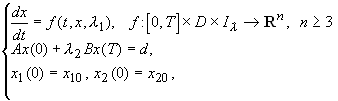(8)
míg Rontó M. [41,47] dolgozataiban a
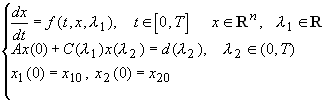(9)
alakú kétpontos paraméteres PÉF esetén található meg a módszer megalapozása, ahol 
ismeretlen skalár paraméterek.
A paraméteres PÉF megoldásain az adott differenciálegyenlet-rendszert és a peremfeltételeket kielégítő 
párokat értjük, ahol 
. Megjegyezzük, hogy a paraméteres PÉF tanulmányozására a szakirodalomban eddig még nem sok módszer ismert és a meglévőkkel a (8) vagy (9) PÉF kezelése számos nehézségbe ütközne. Ezeket a kényelmetlenségeket a (8), (9) PÉF eléggé általános volta és speciális sajátosságai okozzák. Ugyanis a (8) illetve (9) feladat ismeretlen paramétereket tartalmaz, mind a differenciá-legyenlet-rendszerben, mind a peremfeltételekben. Az eddigi kutatások főleg a differenciál-egyenletben meglévő paraméteres eset vizsgálatára irányultak (ld. Feckan M., Stanek S., Luchka A. dolgozatait). Továbbá az adott kétpontos (9) PÉF peremfeltételében az intervallum jobbszélső pontja is paraméter (nem rögzített).
A NAM alapötletének megfelelően az adott (8), (9) feladatokat egy bizonyos, még egy újabb ismeretlen 
paramétert tartalmazó "perturbált" peremérték-feladatra redukáljuk. Ehhez a módosított PÉF -hoz tartozó 
megoldást a szukcesszív approximáció módszerével analitikus formában keressük. Lényeges kiemelni, hogy a "perturbációs" tag mindig egy megfelelő dimenziójú algebrai vagy transzcendens egyenletrendszert (meghatározó egyenletet) generál a 
paraméter értékének és a z vektor komponenseinek előállítására.
A numerikus-analitikus módszer fejlesztésének keretében Rontó M. és Galántai A. [61] a periodikus PÉF esetén egy új eljárást fejlesztettek ki a sorozatos közelítések előállítására. A módosított algoritmus segítségével (ún. kettős iteráció bevezetésével a relaxáció-elv alapján) sikerült egyszerűbben , konstruktív módon felírni a magasabbrendű közelítéseket. Ezentúl elkészült az algoritmus számítógépes programja is, mely bizonyos mértékben hozzájárul a közvetlen számítások egyszerűsítéséhez.
A numerikus-analitikus módszerek általunk kezdeményezett továbbfejlesztésébe bekapcsolódtak a kievi differenciálegyenlet kutatócsoport képviselői is. Együttműködés jött létre az ismert kievi Krilov-Bogoljubov-Mitropolskij-féle nemlineáris mechanikai kutató iskolával a Kievi Tudományegyetem Matematikai-Mechanikai Karának és az Ukrán TA Kievi Matematikai Kutató Intézetének közreműködésével. E közös kutatások eredményeként sikerült enyhíteni a numerikus-analitikus módszerben fellépő elégséges feltételeket, illetve bővíteni a vizsgálandó PÉF - ok osztályait. Így Rontó M. és Trofimchuk S.I. [38,54] megalapozták a NAM periodikus megoldások vizsgálatára ún. Carathéodory-féle
(10)
alakú differenciálegyenletek esetén, ahol 
kompakt halmaz 
-ben, 
pedig a nyílt összefüggő 
halmazhoz tartozó záróburok.
Megjegyezzük, hogy a (10) differenciálegyenlet-rendszert akkor mondjuk Carathéodory-félének a 
tartományban , ha teljesülnek a következő feltételek:
H1) minden 
esetén a 
leképezés Lebesgue-mérhető függvény;
H2) majdnem minden 
esetén az 
függvény folytonos;
H3) létezik olyan mátrix-értékű
függvény, illetve vektor-értékű
függvény 
-beli 
komponensekkel, melyekre minden és majdnem minden 
-re fennáll:
, 
.
Itt az 
jelölés jelentése 
, és a vektorok közötti egyenlőtlenségeket komponensenként vesszük.
Ez esetben az 
függvény Carathéodory-volta lényegesen más technikát igényel a NAM módszer megalapozására, mint az irodalomban eddig vizsgált folytonos esetén.
Nem triviális, de ugyanakkor sokat igérő a NAM általánosítása részben rendezett Banach-térben értelmezett differenciál-, illetve differencia-egyenletekhez rendelt PÉF esetén Rontó M., Rontó A. és Trofimchuk S.I. [39] dolgozatában.
Érdekesség, hogy az új bizonyítási eljárással a már ismert 
-beli folytonos differenciálegyenletekre vonatkozó elégséges feltételeket is sikerült gyengíteni.
Ezenkívül először tudtuk alkalmazni a numerikus-analitikus módszer technikáját autonom differenciálegyenlet-rendszerek periodikus megoldásainál a periódus alsó korlátjának becslésére.
Az együttműködés során Perestyuk M. és Ronto A. [18] cikkében folytatódott a NAM új változatainak kifejesztése másodrendű differenciálegyenlet-rendszerek periodikus megoldásainak tanulmányozására. Rontó A. [26] dolgozatában bizonyította, hogy minden ún. nem-kritikus, integrálható együtthatójú lineáris PÉF -hoz hozzárendelhető egy konvergens numerikus-analitikus módszer.
Rontó M. érdekes és hasznos új összefüggéseket fedezett fel a numerikus-analitikus módszerek és a Cesari-Hale-féle illetve a Cesari-féle módszerek között. Tisztázta az említett módszerek kapcsolatát a Ljapunov-Schmidt-féle eljárással. Nagy számú publikációt gyűjtött össze, melyek a NAM alkalmazásával és fejlesztésével foglalkoznak (több mint 150 tanulmány címszavaiban szerepel a "numerikus-analitikus módszer" kifejezés). Ennek eredményeként "The theory of the numerical-analytic method: Achievements and new trends of development" címmel megszületett Rontó M., Samoilenko A. M. és Trofimchuk S.I. összefoglaló tanulmánya, melynek már mintegy 100 oldalas első négy része 1998-ban publikálásra került [50,51,53,55]. A szóbanforgó tanulmány megfelelő részletességgel és egyes helyeken kritikusan szemlélteti a NAM eddigi eredményeit, fejlődését. Egyben új problémákat is kitűz, illetve hipotéziseket állít fel a módszerrel kapcsolatban.
Így a tanulmány I. része [50] a módszer keletkezését és alkalmazhatóságának feltételeit illetve az utóbbiak finomítását mutatja be periodikus PÉF esetén. Új megvilágításban tárgyalja az adott differenciálegyenlet-rendszer együtthatói szimmetrikus tulajdonságainak hatását a meghatározó egyenletrendszer dimenziójának csökkentésére. Érdekes, eddig nem ismert összefüggéseket közöl a NAM és a Ljapunov-Schmidt-, a Cesari-Hale- és a Cesari-féle eljárásokkal kapcsolatban.
A II. rész [51] a NAM azon változatát tárgyalja, amely elsőrendű egyenlet-rendszerre való visszavezetés nélkül, közvetlenül a másodrendű differenciálegyenlet-rendszerek periodikus megoldásainak egzisztencia vizsgálatára, illetve közelítő meghatározására alkalmas. Ezen túlmenően a dolgozatban sikerült lényegesen javítani egyes becsléseket és a sorozatos közelítések konvergencia feltételeit is. Felhasználtuk az együtthatók egyes szimmetriai tulajdonságait az egzisztencia vizsgálatában.
A III. rész [53] a NAM lehetőségeit retardált, illetve funkcionál-differenciál egyenletekhez rendelt periodikus és általános PÉF esetén tárgyalja. Itt vizsgáljuk, hogy milyen hatása van a késleltetésnek a periodikus megoldás létezésére. Funkcionál-differenciál-egyenletek kétpontos peremérték-feladataira kimutattuk , hogy a megoldás egzisztencia vizsgálata visszavezethető egy integrál-, vagy egy integro-differenciálegyenletre (ez felel meg a absztrakt sémában a "perturbált" feladatnak). Érdekesség, hogy Kwapisz M. és Augusztinowich A. lengyel matematikusok a NAM funkcionál-differenciálegyenlet-rendszerekre való kiterjesztése során dolgozataikban az integro-differenciálegyenletes változatot alkalmazták. Ennek segítségével egyes ún. "nemrezonáló" PÉF esetén sikerült kidolgozniuk a NAM újabb változatait, amelyek nem igénylik a meghatározó egyenletrendszer előállítását és megoldását. Ezt a felfogást egyes dolgozataiban Trofimchuk E.P. illetve Rontó A. ugyancsak alkalmazták különböző PÉF vizsgálatánál.
Az [53] dolgozat ezenkívül egy nem régen bevezetett, nevezetesen "maximumokat" tartalmazó
alakú differenciálegyenlet-rendszer periodikus megoldásainak tanulmányozásával is foglalkozik. Ezeket a vizsgálatokat Bainov D. D. bolgár matematikus társszerzőivel együtt kezdeményezte. Az [53] dolgozatunkban sikerült gyengíteni a konvergenciára vonatkozó általuk megadott elégséges feltételeket.
A szóbanforgó cikkben felvetjük a NAM alkalmazhatóságát a 
alakú operátor egyenlet, illetve annak speciális integro-differenciál eseteire a periodikus megoldások vizsgálata során. Ekkor is sikerült javítani a NAM alkalmazhatósági lehetőségeit az ismert eredményekhez viszonyítva.
A IV. rész [55] bemutatja, hogyan lehet a NAM -t autonóm differenciálegyenlet-rendszerek periodikus megoldásainak vizsgálatára alkalmazni (ez esetben a megoldás periódusa is ismeretlen). Első ízben tárgyaljuk a dolgozatunkban azt, hogyan tükröződik a periodikus megoldás viselkedésében az autonom-rendszer külső T -periodusú hatással való gerjesztése , vagyis létezik-e az egyenletnek T -periodusú periodikus megoldása.
Az [55] dolgozat kitér arra a problémára is, hogy milyen lehetőséget nyújt a NAM ún. impulzusos hatásnak kitett PÉF -ok tanulmányozásában. Ezeket a kutatásokat legelőször az ukrán Peresztyuk N.A. és a bolgár Bainov D. D. professzorok kezdeményezték tanítványaikkal együtt. Mindemelett az [55] cikk szerzői pontosították és finomították az ide vonatkozó egyes eredményeket.
2.2. Kollokációs módszer impulzusos peremérték-feladatokra
Az előző alfejezetben tárgyalt sorozatos közelítésen alapuló numerikus-analitikus módszer végsősoron a PÉF megoldását zárt alakban állítja elő, melynél a megoldások ismeretlen paramétereket tartalmaznak. Ezen paraméterek konkrét értékét az ún. megha- tározó (algebrai, vagy transzcendens) egyenletrendszerek megoldásaként kapjuk.
Így tágabb értelemben a numerikus-analitikus módszerek csoportjába sorolhatnánk a projekciós elven alapuló eljárásokat is (pl. a Galjerkin,- és a kollokációs módszert), melyek egy bizonyos egyenletrendszer numerikus megoldása után szintén zárt alakban adják meg a megoldást. Számunkra itt a továbbiakban a kollokációs módszer a fontos. Ami a kollokációs eljárás keletkezését illeti, az megtalálható pl. a [3,4] monográfiákban. A kollokációs módszer alapgondolata a következő: a vizsgált PÉF megoldását a peremfeltételeket kielégítő, bizonyos alapfüggvények ismeretlen együtthatójú lineáris kombinációjának alakjában keressük. Ezen ismeretlen együtthatókra (első,- vagy magasabbrendű skalár differenciálegyenletek esetén), vagy együttható-vektorokra (első,- vagy magasabbrendű differenciálegyenlet-rendszerekre) előírjuk, hogy a közelítő megoldás a differenciálegyenletet (differenciálegyenlet-rendszert) adott pontokban - az ún. kollokációs helyeken - pontosan elégítse ki.
Így az ismeretlen együtthatókra előálló algebrai egyenletrendszert a kollokáció módszer meghatározó egyenletrendszerének nevezzük. Nyilvánvaló, hogy lineáris PÉF esetén a meghatározó egyenletrendszer lineáris, míg nemlineáris feladadokra nemlineáris. Ha az alapfüggvények algebrai polinomok, akkor algebrai kollokációról, míg trigonometrikus polinomok esetén trigonometrikus kollokációról beszélünk. A trigonometrikus kollokációt periodikus,- míg az algebrai kollokációt általános peremérték-feladatok megoldására célszerű alkalmazni.
Megjegyezzük, hogy nemlineáris kétpontos skalár PÉF megoldására az algebrai kollokációs módszert 1966-ban Vainikko G. dolgozta ki ("On convergency of collocation method for nonlinear differential equations", Zh. vycsisl. Mat. i Mat. Fiz 6, 1966, 35-42 cikkében). Ezzel kapcsolatban ld. még Vainikko G. "Approximative methods for nonlinear equations (Two approaches to the convergence problem)", Nonlinear Analysis: Theory, Methods and Applic., 6, 1978, 644-687 cikkét.
Nemlineáris differenciálegyenlet-rendszerek kétpontos peremérték-feladataira az algebrai kollokáció, illetve a periodikus megoldások előállítására a trigonometrikus kollokációs módszer kifejlesztése 1971-ben Rontó M. dolgozataiban találhatók meg (ezek az eredmények a [3,4,5] monográfiákban is megjelentek).
Így a [3,4] könyvekben a
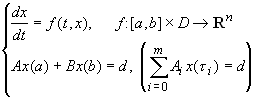(11)
alakú nemlineáris két- vagy többpontos PÉF esetén bizonyítottuk az algebrai kollokáció konvergenciáját, amikor a kollokációs alappontokat egy ortogonális polinomrendszer zérushelyeiből származtatjuk.
Továbbá, ezekben a monográfiákban a periodikus
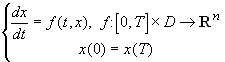(12)
PÉF T -periodikus megoldásának meghatározása során igazoltuk a trigonometrikus kollokáció konvergenciáját is. A (12) feladatban a közelítő megoldást a
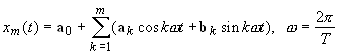(13)
vektor-értékű trigonometrikus vektor-polinom alakjában kerestük, míg a 
számú kollokációs pontot a [0,T) intervallumon ekvidisztáns módon választottuk.
Megjegyezzük, hogy a trigonometrikus kollokáció konvergenciájának bizonyításánál feltételeztük, hogy a (12) PÉF rendelkezik T - periódusú 
megoldással és ezek után igazoltuk, hogy létezik (13) alakú közelítő megoldása és 
. Érdekesség, hogy a [3,4] monográfiában elsőként vetettük fel és meg is oldottuk a fordított feladatot: a (13)-s alakú közelítő megoldás létezéséből megfelelő feltételek mellett levezettük a pontos T -periódusú 
megoldás létezését.
Ezenkívül kidolgoztuk a trigonometrikus kollokáció új változatát, melyben egy mátrix-vektor technika segítéségével a meghatározó egyenletrendszert nem az ismeretlen 
együttható-vektorra írtuk fel, hanem a (13) -as polinomnak az ekvidisztáns kollokációs pontokban vett
értékvektorára.
A későbbiekben az [5] monográfiában kifejlesztettük a trigonometrikus kollokációt nemlineáris késleltetett argumentumú
differenciálegyenlet-rendszer esetére, csakúgy, mint az algebrai kollokációt a
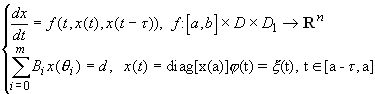
retardált argumentumú többpontos PÉF esetére.
A kollokáció módszer újabb feladatokra való kiterjesztésével foglalkoznak Rontó M. és Putyatyina T.V.[16,17] cikkei. Ezekben a dolgozatokban az a lényeges, hogy a perem-feltételekben határozott integrál szerepel, melynek az integrandusza az ismeretlen függvényt tartalmazza. Az ilyen típusú feltételek a többpontos peremfeltételek "határesetének" is tekinthetők. Az integrált tartalmazó peremfeltételek mellett is sikerült megkonstruálnunk a kollokáció módszer konvergenciájának bizonyítása során fellépő lineáris homogén PÉF Green-féle függvényét.
Samoilenko A.M, Ronto M. és Kurbanbaev O. [7,9] dolgozataiban illetve Samoilenko A.M, Ronto M. [6] monográfiájában kidolgozták a trigonometrikus illetve algebrai kollokációt a peremérték-feladatok újabb osztályaira, nevezetesen a következő típusú egy- vagy több impulzusos közönséges differenciálegyenletekhez rendelt PÉF megoldásainak meghatározására:
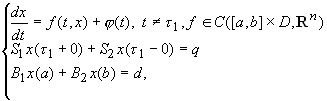
ahol
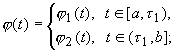
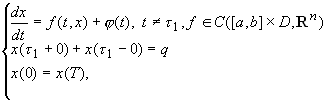
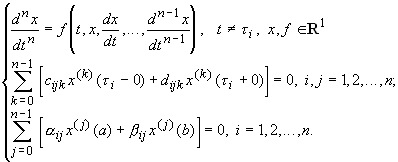
Az említett dolgozatokból kiindulva Rontó M. és Tuzson Á. [21] cikkükben az alábbi szakaszosan folytonos jobboldallal rendelkező impulzusos peremérték-feladatra általánosították a kollokációs módszert:
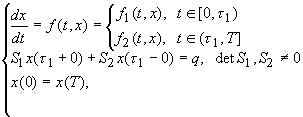(14)
ahol 
zárt korlátos tartomány.
Előkészítésként a [21] dolgozatban megkonstruáltuk a megfelelő lineáris homogén impulzusos PÉF Green-féle függvényét.
A trigonometrikus kollokációnak megfelelően a (14) periodikus, impulzusos PÉF közelítő megoldását m- edfokú
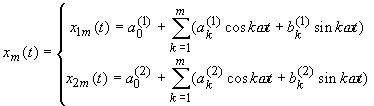
(15)
szakaszosan folytonos trigonometrikus polinom alakjában kerestük, ahol 
, 
számú ismeretlen vektor-együtt-hatók.
Az utóbbiak előállítására az
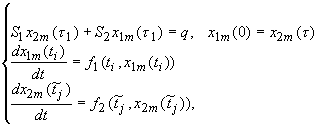(16)
meghatározó algebra egyenletrendszer megoldására volt szükség, ahol a kollokációs pontok
Továbbá Rontó M. és Tuzson Á. [32,35] cikkeikben kidolgoztak egy olyan mátrix-vektor technikát, mely jól algoritmizálható és nagymértékben egyszerűsíti a (16) meghatározó egyenletrendszer előállítását, mind az együttható-, mind az értékvektorra és elősegíti azok numerikus megoldását. Ez az eljárás hasonló a [3,4] monográfiákban kidolgozott impulzusmentes peremérték-feladatokra vonatkozó mátrix-vektor műveletrend-szerhez.
Tuzson Á. [29] cikkében igazolta az algebrai kollokáció konvergenciáját a következő kétpontos, 1 -impulzusos, nemlineáris PÉF esetére:
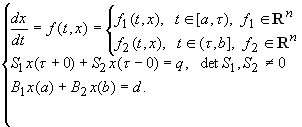
Továbbá Tuzson Á. [34] dolgozatában kiterjesztette a [32] cikkben kifejlesztett módosított trigonometrikus kollokációt és a szükséges mátrix-műveletrendszert az alábbi
n -edrendű impulzusos (skalár) differenciálegyenletekhez rendelt periodikus peremérték-feladatokra:
A fentiekben felsorolt eredmények olyan impulzusos differenciálegyenletekre vonatkoztak, amelyekben az impulzusos hatás rögzített pontban vagy pontokban lép fel. Rontó M. és Trifimchuk S.I. [26] dolgozata egy lényegesen általánosabb, Banach-térben értelmezett impulzusos differenciálegynlet T - periódusú megoldását tanulmányozza, nem rögzített időpontbeli impulzusos hatás mellett:
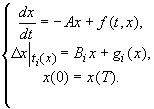(17)
A (17) feladathoz a következő értelmezés tartozik:
X Banach-tér, A az X térben értelmezett lineáris operátor,
adott lineáris operátorok, 
.
Az impulzusos hatás akkor érvényesül, ha a megoldás a 
hyperfelületeken halad át és 
bizonyos tulajdonságokat kielégítő nemlineáris függvény. Az ún. Poincare-féle leképezés technikájával a [26] dolgozatban sikerült bizonyítani a (17) impulzusos feladat szakaszosan folytonos T -periódusú megoldásainak a létezését.
Továbbá bizonyos feltételekkel biztosítottuk a T -periódusú megoldás unicitását és exponenciális stabilitását.
2.3. Összefoglaló megjegyzések
A differenciálegyenlet csoport tagjai a numerikus-analitikus illetve a kollokációs módszerrel kapcsolatos eredményeiket számos nemzetközi konferencia előadásain is ismertették: Rontó M. [15, 27, 31, 45, 48, 49, 52], Rontó M. és Tégen M. [19, 25, 46], Rontó M. és Tuzson Á. [32, 35], Tégen R.M. [37], Rontó M. és Rontó A. [30, 40], Tuzson Á. [20], Rontó M. és Mészáros J. [42].
Megjegyezzük, hogy a numerikus-analitikus módszer technikájával sikerült olyan állításokat bizonyítani, melyek jelentőségekkel bírnak más módszereknél is. Így Farkas M. "Periodic motions" (New York: Springer, 1994) c. monográfiájában a pertubációs módszerben felhasználta és ismertette a periodikus megoldások létezésére vonatkozó egyik
- a [4] könyvből származó - egzisztencia tételünket.
Tudomásunk van olyan 24 kandidátusi disszertációról, amelyekben felhasználták a numerikus-analitikus módszerekkel kapcsolatos eredményeinket. Ezentúl dolgozatainkra mintegy 400 hivatkozást tartunk számon.
Imponáló az a tény, hogy egyes kutatóműhelyekben elkezdtek részben foglalkozni a numerikus-analitikus módszerekkel is. Ennek kapcsán pl. megemlíteném a Kwapisz M. prof. által irányított gdanski (Lengyelország) csoportot, a Zabreiko P. prof. vezetése alatt működő minszki (Fehéroroszország) kutatókat, a Bainov D.D. prof. Bulgáriában működő kutató iskoláját.
Megemlítjük, hogy már elkészült Rontó M. és Samoilenko A. "Numerical-analytic methods in the theory of boundary- value problems" című angol nyelvű monográfiájának a kézirata, amely a szóbanforgó numerikus-amalitikus technika segítségével elért újabb eredményeket szándékozik bemutatni. A World Scientific Publishing Kiadó jóvoltából a könyv megjelenése 1999-ben várható.
A szerző tudományos vezetése mellett a csoport tagjai közül 1997-ben ketten megszerezték a Ph.D tudományos fokozatot:
- Raisz Péterné ("Numerikus-analitikus módszer többpontos peremérték-probléma
megoldására és műszaki alkalmazása")
- Tóth Lajosné Tuzson Ágnes ('Munkásság tézisszerű összefoglalása").
Emellett a szóbanforgó témakörökben a szerző tudományos vezetése mellett korábban heten védték meg kandidátusi disszertációjukat:
- Kurbanbajev O. ("Impulzusos hatású peremérték-feladatok", 1990);
- Dzsigun E. ("Magasabbrendű differenciálegyenletek alkalmazása áramkörök modellezésében", 1991);
- Martinyuk S. ("Nemlineáris egyenletrendszerekhez rendelt peremérték-feladatok vizsgálata", 1992);
- Putyatyina T. ("Nemlineáris peremérték-feladatok vizsgálata kollokációs módszerrel", 1993);
-Martinyuk O. ("Peremérték-feladatok megszámlálhatóan végtelen sok nemlineáris differenciálegyenletek esetén", 1993);
- Szavina T. ("Numerikus-analitikus módszer többpontos peremérték-feladatokra", 1996);
- Korol I. ("Paramétereket tartalmazó peremérték-feladatok vizsgálata", 1996).
Részben az itt ismertetett témakörben elért eredmények szolgálták az alapját annak,hogy 1996-ban a jelen sorok szerzője tagja lehetett annak a 8 tagú nemzetközi kutató csoportnak, amely Ukrán Állami Díjban részesült a Tudomány és Technika területén a "Nemlineáris analízis új matematikai módszerei" c. kutatásukért. (A kitüntetésben részesült csoport tagjai: Mitropolskij Ju. A. akadémikus, Samoilenko M.A. akadémikus, prof. Kulic V.L., prof. Lopatin O.K., prof. Rontó M., prof . Perestyuk M.O., prof. Teplinskij Ju. V., prof. Nguen Van Dao).
Mindezek után talán megállapítható, hogy az Analízis Tanszék Differenciálegyenlet-csoport eddigi eredményei hazai és nemzetközi elismerésben is részesültek, amely hozzájárult ahhoz, hogy a Tanszéket a szóbanforgó szakterületen tudományos műhelyként jegyezzék.
Irodalomjegyzék